Abstract [1]

Computerized tomography (CT) is a non-invasive imaging technique that allows to examine slices of the human body without damaging it. The human body is X-rayed from several angles, producing a set of X-ray projections, the so-called sinogram. Each sinogram column corresponds to the X-ray projection at one angle. Computerized tomographic reconstruction calculates from this set of 1D sinogram lines a reconstructed 2D image, a slice through the internal structure of the examined body. This report discusses and compares in detail several CT image reconstruction techniques. Its main contribution is the implementation and extension of the standard filtered backprojection algorithm by using splines and least-squares approximation within the general framework of Hilbert spaces and spline bases.

The standard filter backprojection (FBP) technique filters each sinogram column with the ramp filter. The ramp filter 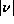compensates for the blur introduced by summing up the backprojections of all sinogram lines. The FBP algorithm is well defined in the continuous domain, but for the discrete implementation interpolation problems arise in both the filtering and backprojection part. This work presents several solutions to circumvent these.

An algorithm to generate sinograms from the test images was implemented using the Radon transform. The reconstructed images from the sinogram are then compared to the original test image to evaluate the quality of the discussed reconstruction algorithms. The widely used standard FBP algorithm was implemented as described in [5] and [6]. The discrete implementation of the ramp filter uses the standard Fast Fourier Transform (FFT). The high-pass nature of the ramp filter gives rise to noise amplification. In practice modified filters are designed to handle this problem. Well established, but rather ad-hoc modified ramp filters are the Shepp-Logan, Hamming and Cosine filter [5].

The standard FBP algorithm interpolates (linearly) the filtered sinogram lines before backprojecting them. A more general interpolation scheme using a splines expansion of higher degrees was implemented. Two different ways to obtain the coefficients of the expansion were investigated: by introducing a supplementary recursive filtering step [4] and by modifying the ramp filter.

The filtered backprojection can be reformulated as a least-squares approximation problem, where the image is approximated in a spline space [3]. For each approximation space an optimal least-squares modified ramp filter can be deduced.

Another approach applies approximation in spline spaces not only to the image, but to the sinogram columns as well. Then the projection (and backprojection respectively) corresponds to the evaluation of a spline tri-kernel: the convolution of three scaled B-splines [2]. This enables to efficiently implement both the Radon transform and the optimal least-squares back projection with splines of up to degree 5.

All algorithms were implemented in C and tested for different approximation degrees. They allow great flexibility as their precision can be arbitrarily enhanced by taking higher order approximation spaces. However, the price to pay is an increase of the computational cost. Nevertheless, it is more efficient to take a better interpolation scheme than taking a finer sampling step.

Résumé [1]

La tomographie computerisée (CT) est une technique d'imagerie non-invasive qui permet d'examiner des coupes du corps humain sans l'endommager. Le corps à examiner est radiographié depuis plusieurs angles, produisant un ensemble de projections de rayons X, appelé sinogramme. Chaque colonne du sinogramme correspond à une projection pour un angle donné .

A partir du sinogramme, la reconstruction tomographique computerisée calcule l'image 2D d'une coupe au travers de la structure interne du corps examiné.

Le présent travail compare et discute plusieurs techniques de reconstruction d'images CT. Sa contribution principale est l'implémentation et l'extension de l'algorithme standard de rétroprojection filtrée à l'aide des splines et de l'approximation au sens des moindres carrés.

La technique standard de rétroprojection filtrée (FBP) filtre chaque colonne du sinogramme avec le filtre de rampe 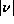. L'algorithme de FBP est bien défini dans le domaine continu, mais des problèmes d'interpolation surgissent lors de son implémentation discrète, aussi bien dans le filtrage que dans la rétroprojection elle-même. Le présent travail présente plusieurs approches pour pallier à ces problèmes. Elles sont basées sur le principe de l'approximation des moindres carrés tout en se plaçant dans le cadre général des espaces de Hilbert et des bases de splines.

Un algorithme pour générer des sinogrammes d'images d'essai a été mis au point en utilisant la transformée de Radon. Les images reconstruites du sinogramme sont alors comparées avec l'image initiale d'essai pour évaluer la qualité des algorithmes de reconstruction discutés.

L'algorithme standard très répandu de FBP a été implémenté comme décrit dans [5] et [6].

L'implémentation discrète du filtre de rampe utilise la transformée de Fourier rapide standard (FFT). Le caractère passe-haut du filtre de rampe donne lieu à une amplification du bruit à haute fréquence. Aussi, la réponse fréquentielle des filtres utilisés dans la pratique décroÓt pour les hautes fréquences, afin de supprimer ce bruit. Parmi les filtres de rampe les plus connus, on peut citer les filtres de Shepp-Logan, de Hamming et cosinus [5].

L'algorithme standard de FBP interpole (linéairement) les colonnes filtrées du sinogramme avant de les rétroprojeter. Un schéma d'interpolation plus général utilisant un développement du signal en une somme de splines de degrés plus élevés a été implanté. Deux approches différentes pour obtenir les coefficients du développement des colonnes du sinogramme ont été étudiées: D'abord la modification du filtre de rampe puis un filtrage récursif [4] supplémentaire qui permet d'effectuer le passage entre les espaces de splines.

La rétroprojection filtrée peut être reformulée comme problème d'approximation par moindres carrés où l'image est approchée dans un espace de splines, par exemple. Pour chaque espace d'approximation on peut déduire un filtre de rampe modifié optimal au sens des moindres carrés [3].

Une autre approche applique l'approximation dans des espaces de splines non seulement sur l'image, mais également sur les colonnes du sinogramme. Alors la projection aussi bien que la rétroprojection correspondent à l'évaluation d'un tri-kernel de splines, soit à la convolution de trois B-splines normés [2]. Ceux-ci permettent d'implanter de manière efficace la transformée de Radon aussi bien que la rétroprojection optimale au sens des moindres carrés avec des splines de degrés allant jusqu'à 5. Tous les algorithmes ont été implémentés en C et testés pour divers degrés d'approximation. Ils permettent une grande flexibilité par le fait que leur précision peut être augmentée à volonté en choisissant des espaces d'approximation d'ordre plus élevé. Ceci se monnaye bien entendu en temps calcul. Cependant, il est plus efficace d'utiliser un meilleur schéma d'interpolation que de diminuer le pas d'échantillonnage.

Zusammenfassung [1]

Computer Tomographie (CT) ist ein nicht invasives Verfahren, womit Querschnitte des menschlichen Körpers betrachtet werden, ohne diesen zu verletzen. Der zu untersuchende Körper wird unter verschiedenen Winkeln geröntgt und anschliessend wird ein Satz von Röntgenstrahlprojektionen, das sogenannte Sinogramm erstellt. Jede Kolonne des Sinogramms entspricht der Röntgenstrahlprojektion eines Winkels. Computer Tomographie Rekonstruktion errechnet aus dem Sinogram wieder ein zwei-dimensionales Bild, das einen beliebigen Schnitt durch die interne Struktur des untersuchten Körpers darstellt.

Vorliegende Diplomarbeit behandelt und vergleicht mehrere CT-Bild-Rekonstruktiontechniken. Ihr Hauptbeitrag ist die Implementierung und die Erweiterung des gefilterten Rückprojektions- Standardalgorithmus durch Splines und Kleinste-Quadrate Approximation.

Die Technik der Standardfilter Rückprojektion (FBP) filtert jede Sinogrammkolonne mit einem Rampenfilter. Der Rampen Filter 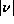kompensiert die Unschärfe, die durch das Aufsummieren der Rückprojektionen aller Sinogrammzeilen entsteht. Der FBP-Algorithmus ist im kontinuierlichen Bereich exakt, wird er jedoch diskret Implementiert, so treten Interpolationsprobleme sowohl beim Filtern, als auch bei der Rückprojektion auf.

Vorliegende Arbeit stellt diese Probleme in den allgemeinen Rahmen der Hilberträume und der Splinebasen und basieren auf der Approximation nach dem Prinzip der kleinsten Quadrate.

Zur Berechnung des Sinogramms der Testbilder wurde die Radon Transformation verwendet. Die aus dem Sinogramm rekonstruierten Bilder werden mit dem ursprünglichen Testbild verglichen, um die Qualität der betrachteten Rekonstruktionalgorithmen zu beurteilen. Die diskrete Implementation der Rampenfilter verwendet die schnelle Fourier Transformation (FFT).

Die Hochpassnatur der Rampenfilter erzeugt hochfrequentes Rauschen, das durch Modifizieren der Filterfrequenzgänge zu unterdr¸cken ist. Wohlbekannte modifizierte Rampen-Filter sind der Shepp-Logan-, der Hamming- und der Cosine-Filter (siehe [5] und [6]).

Der Standard FBP-Algorithmus interpoliert (linear) die gefilterten Sinogrammzeilen, bevor er sie rückprojiziert. Ein allgemeinerer, auf der Spline Expansion höheren Grades basierender Interpolationsansatz wurde implementiert. Zwei unterschiedliche Möglichkeiten, die Koeffizienten der Sinogrammzeilen Expansion zu gewinnen, wurden untersucht: Erstens ein zusätzlicher rekursiver Filter [4] zwischen den Splineräumen, zweitens eine Modifikation des Rampenfilters.

Die gefilterte Rückprojektion kann ebenfalls als Kleinste-Quadrate Approximationsproblem umformuliert werden, worin das Bild etwa in einem Spline-Raum approximiert wird. Für jeden Approximationsraum kann daraus ein modifizierter Rampenfilter abgeleitet werden [3].

Ein anderer Ansatz besteht darin, die Approximation in Spline-Räumen nicht nur auf das Bild, sondern ebenfalls auf die Sinogramm-Linien anzuwenden. Die Projektion, bzw. die Rückprojektion entsprechen dann der Auswertung eines Spline Tri-Kernels, also der Faltung dreier skalierter B-Splines [2]. Damit wurde die Radon-Transformation und die optimale Kleinste-Quadrate Rückprojektion mit Splines bis zu füntem Grades effizient realisiert.

Alle Algorithmen wurden in C implementiert und für verschiedene Approximationsgrade getestet. Dadurch wird eine grosse Flexibilität erreicht, zumal die Präzision durch die Wahl von Approximationsräumen höherer Ordnung verbessert werden kann. Dies ist allerdings mit Rechenzeit zu berappen. Immerhin ist es effizienter, ein besseres Interpolationsschema zu verwenden, als den Abtastschritt zu verkleinern.

About this document ...

This document was generated using the LaTeX2HTML translator Version 96.1-h (September 30, 1996) Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.

The command line arguments were:
latex2html -html_version 2.0 -split 0 -no_navigation abstracts.tex