Performs a non-redundant fractional wavelets transform of an image. The wavelet basis is specified within the family of fractional splines, which are the only wavelets to date that are tunable in a continuous fashion. Experiments this new family of wavelets with the plug-in of the public-domain software ImageJ.
Important note: You are free to use this software for research purposes, but you should not redistribute it without our consent. In addition, we expect you to include adequate citations and acknowledgments whenever you present or publish results that are based on it.
M. Unser, T. Blu, "Fractional Splines and Wavelets," SIAM Review, vol. 42, no. 1, pp. 43-67, March 2000.
T. Blu, M. Unser, "The Fractional Spline Wavelet Transform: Definition and Implementation," Proceedings of the Twenty-Fifth IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP'00), Istanbul, Turkey, June 5-9, 2000, vol. I, pp. 512-515.
T. Blu, M. Unser, "A Complete Family of Scaling Functions: The (α, τ)-Fractional Splines," Proceedings of the Twenty-Eighth IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP'03), Hong Kong SAR, People's Republic of China, April 6-10, 2003, in press.
Open an image
The Wavelet Transform plug-in for ImageJ only works with images (no image sequences).
- Open an image or image sequence using the standard menu of ImageJ: File->Open...
- Click on the image frame to put it in focus and then start the plug-in by selecting: Plugins->Fractional Spline Wavelet->Wavelet Transform
- Now the plug-in is started and all operations will be done on the image or image sequence last in focus
Functioning of the Wavelet Transform plug-in
- The plug-in operates in two modes:
1. Analysis: compute the wavelet transform analysis
2. Synthesis: computing the inverse discrete wavelet transform - Any processing using ImageJ can be done on the wavelet coefficients before reconstruction since the plug-in window is not kept modal.
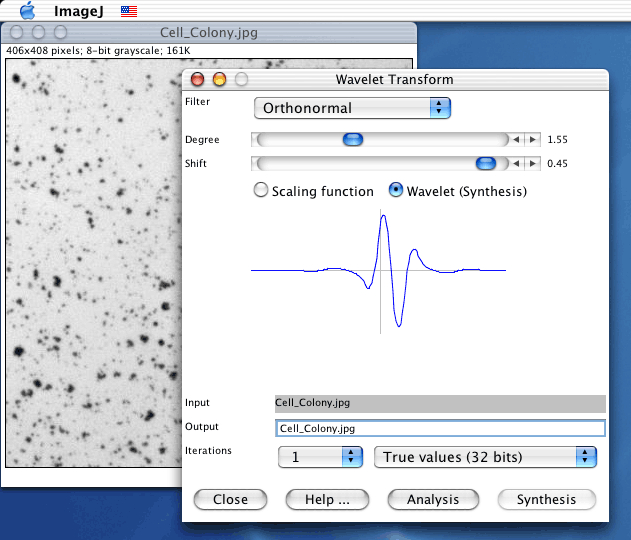
Step 1 - Discrete Wavelet Transform: Analysis side
The complete family of (bi)-orthogonal spline wavelets with fractional degree (α) and arbitrary shift (τ) is available in this plug-in
- Filter: orthonormal (filters for analysis and synthesis are equal), biorthogonal (B-spline at the analysis or the synthesis side, the dual the other way around);
- Iterations: can be selected independently for each of the three dimensions; if one selects 0, no transform in this dimension will be done;
- Degree: the fractional degree of the spline can be selected, for Haar wavelets select degree 0.0 and shift 0.50;
- Shift: the shift of the spline function (0.0 results into symmetrical filters).
The scaling function or the wavelet are displayed in the central part of the plug-in window. In this way, the user can visualize the effects of changing the transform parameters.
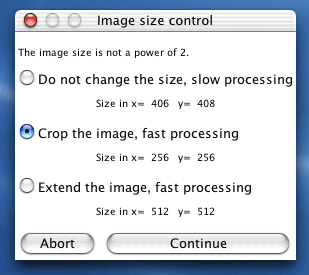
When the image dimensions are not powers of two, an "Image size control" window allows you to crop or extend the original image dimensions. If the size is not a power of two, the algorithm still works but the processing will be very slow.
Optionally - Processing
You can use any ImageJ manipulations to process the wavelet coefficients
Step 2 - Inverse Discrete Wavelet Transform: Synthesis side
The final step reconstructs the (processed) image or image sequence using the same settings as the analysis side