Online Image Processing Demonstrations
Image Processing Online Demonstrations
These demonstrations run on any moderm browsers supporting HTML5.
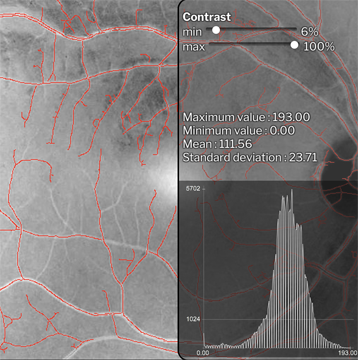
Ridge Detector
Detection of the ridges in an image using the Hessian filter (Canny algorithm).
Reference

Fourier Filtering
Filtering an image in the frequency domain. Low-Pass, high-Pass, or band-Pass filters.

Gradient Structure Tensor
Directional analysis of an image based on the gradient structure tensor.
Read more
Reference
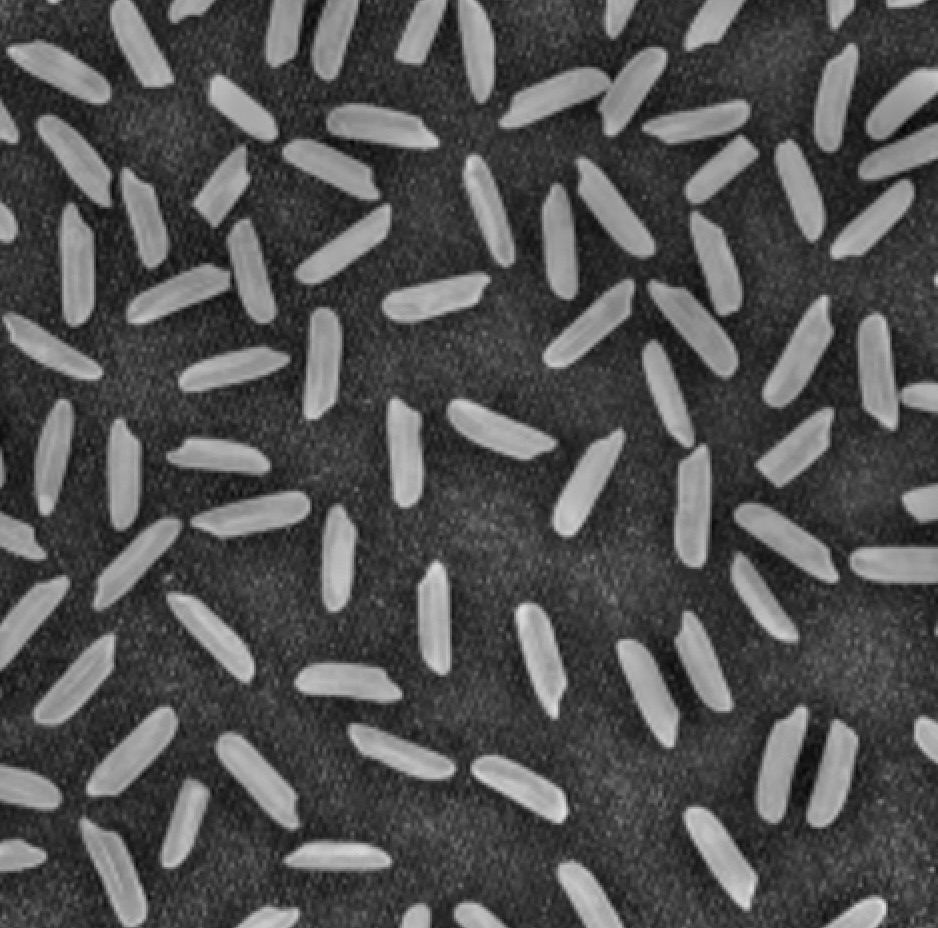
Local Normalization
Uniformization of the local mean and variance. Correct the non uniform illumination.
Read more
Reference

Graylevel Watershed
Run the watershed segmentation algorithm on a smoothed version of the image.
Read more
Reference

Morphological Operators
Classic morphological operators running on graylevel image.
Reference

Fast Fourier Transform
Discrete Fourier transform of a image. Display modulus, phase, real, and imaginary part.
Apple iOS Apps
These Apple apps are available on the Apple store and run on iPhone/iPad.

Filter Creator
Filter Creator helps you to better understand the mathematics of discrete and continuous audio filters and is particularly aimed at students of signal processing classes.

iMondrian
This app generates artistic representations of Mondrian processes. These processes are named after Piet Mondrian (1872-1944), a great figure in the neoplasticism style known for his grid-based paintings.

3D Screen Saver
Mondriaan process mapped onto the surface of an exponential-spline monopole Download
Java Applets
These Java applets are running on browsers supporting a recent Java Virtual Machine.
SURE-LET Wavelet Denoising
(in color or in grayscale)Florian Luisier
A new approach to color or grayscale image denoising.Variational Levelset Spline
Olivier Bernard
New formulation of level-set modeling the implicit as a continuous parametric function expressed on a B-spline basis.Steerable Feature Detection
Mathews Jacob and François Aguet
General approach for the design of 2-D feature detectors.Extended Depth of Field using the Wavelet Transform
Download a program to perform an extended depth of focus of z-stack images to obtain in focus image.Hex-splines
Dimitri Van de Ville
A novel spline family for hexagonal lattices.Fractional Splines Wavelets
Thierry Blu
Wavelet bases with a continuously-varying order parameter and continuously-varying order and shift parameters.Computerized Tomography
Michael Liebling
Simulates the computerized tomography (Radon transform) and performs the reconstruction (filtered backprojection).Comparison of interpolators
Philippe Thévenaz
Compares the standard interpolation functions with the ones developped by the BIG.Fractional Quincunx Wavelets
Manuela Feilner
Shows the quincunx transform using filters of fractional order.Resizing
Arrate Muñoz Barrutia
The optimal algorithm to resize images.Spline Warping of our staff members
Daniel Sage
Bidirectional landmark warping of our staff.Edge Detection
(Move to HTML5/Javascript) The old applet is still available at this pageDaniel Sage
Gradient
Daniel SageBasis functions of the FFT
Daniel SageBasis functions of the DCT
Daniel SageBasis functions of the Haar Wavelet Transform
Daniel Sage
Local Normalization
(Move to HTML5/Javascript) The old applet is still available at this pageDaniel Sage
Morphology Operators
(Move to HTML5/Javascript)The old applet is still available at this page
Daniel Sage
Smoothing Techniques
Daniel SageTemplate Matching
Daniel SageDrop Shape Analysis
Aurélien StalderDenoising of fractal-like images using Polyharmonic B-splines
Alex PrudencioFiltering in Fourier Domain
(Move to HTML5/Javascript)The old applet is still available at this page
Joy Anushini Ariarajah
Edge detection with a sub-pixel precision
Nicolas PavillonComplex Fractional Splines Wavelet
Florian LuisierVirtual Microscope
Christophe MagnardDiffusion Enhancing Methods
Alwyn FernandesContinuous Wavelet Transform using Splines
Raphaël ErtleGraylevel Watershed
(Move to HTML5/Javascript) The old applet is still available at this pageDaniel Stadelmann
Non Linear Diffusion Filtering
Laurent Vieira De MelloInterpolation on Affine Transformation
Raphaël Marthe
Mathematica CDF Player
Requires the CDF Player of Wolfram Mathematica.
Exploration of the B-Spline

This website visualizes some useful applications of Polynomial Splines, also called B-splines.
Robin Lang and Daniel Schmitter, 2017.