Digital Filtering

Java Notes
Absolute value	y = \|x\|	y = Math.abs(x);
Power elevation	y = x^a	y = Math.pow(x, a);
Exponential functions	y = e^a	y = Math.exp(a)
Number Pi	π	double pi = Math.PI;
Closest integer of x		int y = (int)Math.round(x);
Largest integer of x		int y = (int)Math.ceil(x);

1. Implementation of the 3x3 moving-average filter

The 3x3 moving-average filter replaces a pixel by its average in a 3x3 centered window. There are several ways to implement a moving-average filter. We provide three versions of the implementation and one version is :

MA3x3 NonSeparable plugin: The 3x3 window is scanned for each pixel of the image (mirror boundary conditions are applied);
MA3x3 Separable plugin: The moving-average routine is implemented in 1D. It is applied to all rows and to all columns (mirror boundary conditions are applied);
Convolver of ImageJ command: Find the mask of the 3x3 moving-average and write it in the window Convolver of ImageJ (menu Process→Filter→Convolve).

Read and understand the code of two plugin versions of the moving average filter in Code.java

Apply the three routines on the stack of images "cell-zstack.tif" and compare the results of the three versions in terms of time computation and image content. Fill in the report.

2. Implementation of filters

Implements the filters below. If it is a separable filter, implement it in a separable way, while taking proper care of the boundaries (mirror conditions).

2.1 Filter A

Write a method doFilterA() that implements the filter defined by the following mask.
What is the effect of the filter ? Fill in the report.

2.2 Filter B

Write a method doFilterB() that implements the filter defined by the following mask.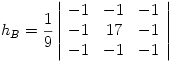
What is the effect of the filter ? Fill in the report.

2.3 Filter C

Write a method doFilterC() that implements the filter defined by the following mask.
What is the effect of the filter ? Fill in the report.

2.4 Filter D: Southeast shadows filter

Write a method doFilterD() that produces a Southeast shadows effect on an image.
The goal is to obtain exactly the same output image than the function Southeast Shadows of ImageJ (menu Process→Shadows→Southeast). Evaluate the difference between your result and the output of ImageJ command. Fill in the report.
Hint: Observe the response of the isolated pixel (bottom of the "boats.tif" image) to deduce the impulse response of the filter and to find the corresponding mask.

3. Detection of spots

Here, we propose to detect the brightest cities (bright spots) on a part of the world image "earth.tif" provided by a satelitte. Convert this image in grayscale image (menu Image→Type→8-bit).
To acheive this goal, we will use the DoG filter (Difference of Gaussians) as a bright spots detector. The DoG is constructed from the subtraction of two different Gaussian functions: DoG(x) = h_σ1(x) - h_σ2(x) given the following profile in 1D (thick line).

a. Gaussian filter

First, we have to implement the 2D Gaussian filter h_σ where the standard deviation σ controlles the smoothing strength. We propose to discretize the 2D Gaussian function between [-3*σ,3*σ].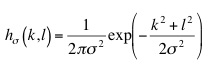

To simplify the implementation, we choose a size of the filter equal to n = (int)(2*ceil(3*σ))+1, hence n is always odd. Write a method doGaussian() that convolves an image with this Gaussian filter as non-separable or separable way.
Check the Gaussian filter using Gaussian plugin.

b. Difference of Gaussian

Write a method doDoG() that implements the DoG by calling two times the Gaussian filter and making the substraction. We choose σ₂ = 2 . σ₁. Check the DoG filter using DoG plugin.

c. Application to the spot detection

Apply the DoG filter and the threshold T (menu Image→Adjust→Threshold).

Find the parameters σ₁ and T to detect the brightest cities (around 50 ±20 cities) in the pictureand fill the report.