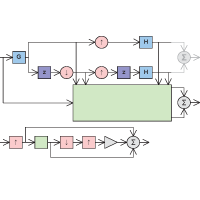
Image reduction and magnification are two faces of the same coin. If one masters the operation M that magnifies a small image f to obtain a large image F = M(f), then the reduction of an image G can be stated as the search for the image g that satisfies G = M(g). These processes are well understood in a linear framework. For instance, magnifying (or reducing) a discrete image f using discrete Fourier techniques can be achieved by padding (or cropping) the discrete Fourier transform of f. In this case obviously, the question arises as to how one should pad the Fourier domain when performing a magnification. Clearly, any arbitrary choice is acceptable, not only the constant value zero, but also any sort of nontrivial and non-constant Fourier padding. However, even if the mathematics dictate that every one of these choices is acceptable, some will work perceptually better than others when applied to images.

In this project, the student is going to explore two approaches to double the linear dimensions of an image while introducing a controlled component belonging to the null space of the reduction operator. In the first case (upper system of the figure), a lazy wavelet transform will be sandwiched between a lowpass analysis filter G and a finite-support synthesis filter H that are the inverse of one another. Since each branch of the global system acts as an independent antialiasing/sampling system, it is possible to learn (large green box), by reducing an image, how best to actually magnify it. In the second case (lower system of the figure), the residue of a nonlinear edge-enhancing operation (small green box) will be added to the signal to populate the null-space of the reduction operator.

Type of work: mathematical filter design and Java programming with ImageJ
Prerequisites: to follow or to have followed the course on image processing taught by M. Unser