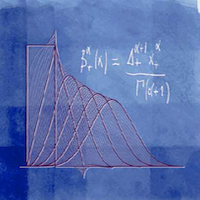
Continuous-domain signals can be reconstructed from their discrete measurements using variational approaches. The reconstructed signal is then defined as a minimizer of a functional, which is composed of a convex combination of two terms, namely data-fidelity (quadratic) and regularization. We have recently proved that when using the L1 norm for the regularization, this reconstructed signal is sparse in the continuous-domain. The sparsity is enforced via a regularization operator: for example, the derivative leads to piecewise-constant solutions (total variation), while the second derivative yields piecewise-linear solutions. The goal of this project is to investigate novel regularization operators, namely fractional derivatives which allow us to vary continuously e.g. between the derivative and the second order derivative. The work would also include the design and implementation of an algorithm for signal reconstruction. The student should have strong mathematical interests (particularly in functional analysis), and basic knowledge of optimization theory.