| Yann Barbotin | Semester project |
| I&C School, EPFL | January 2008 |
Polyharmonic B-splines are a multidimensional generalization of B-splines with interesting applications such as interpolation and design of orthogonal wavelet basis [1][2].
One of the main issue is the computation of the autocorrelation sequence Aφγ necessary to build the orthogonal and interpolant version of the spline, see Figure (1) for example.
Polyharmonic B-splines have infinite support in the frequency domain, and may decay slowly for γ → 1,
thus direct computation of the autocorrelation formula yields an important error ![O[R^(γ-1)]](./figs/slow_cvg.png)
considering terms at a distance less or equal to R from the origin.
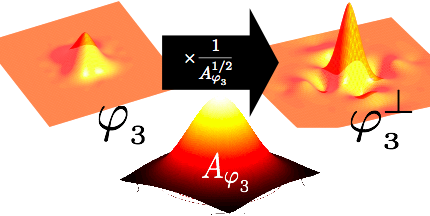
Figure (1) - How to build an orthogonal polyharmonic B-spline (γ=3) with its autocorrelation sequence.
Some inspiration can be found in cristalography [3], namely computation of potential at the boundaries of cristal structures. Adaptation of these technics, resulted in Proposition 1.
Error after truncation is ![O[e^(R^2)]](./figs/fast_cvg.png)
.
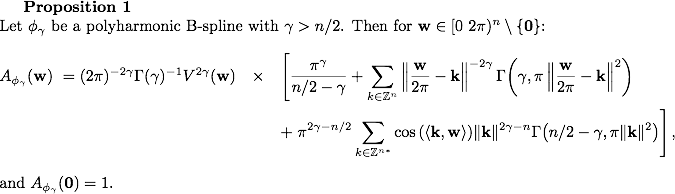
The result is an important gain in speed and accuracy, as illustrated in Figure (2). Moreover performance of this method weakly depend of γ. A 4 pages paper is being written for publication in a signal processing publication.
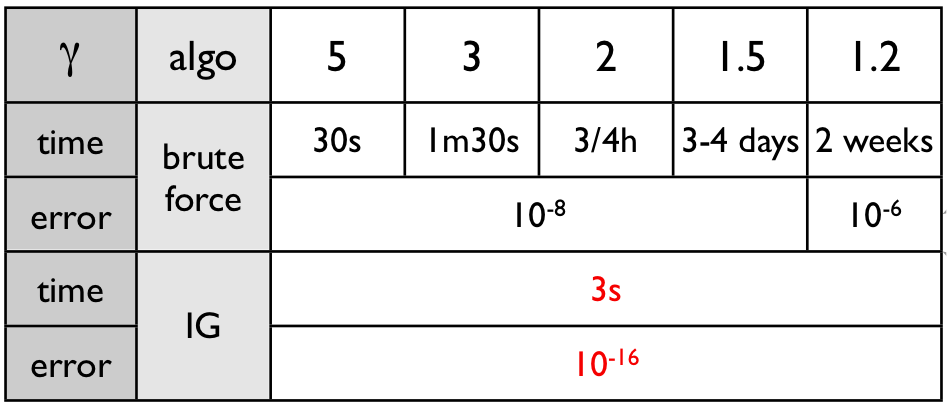
Figure (2) - Comparison of time and accuracy performances between the direct formula algorithm (brute force) and the fast formula one (IG).
[1] D. Van de Ville, T. Blu, M. Unser, "Isotropic Polyharmonic B-splines: Scaling Functions and Wavelets" , IEEE Transactions on Image Processing, 14-11, 2005.
[2] T. Blu, M. Unser, "Fractional Splines and Wavelets" , SIAM review, 42-1, 43--67, 2000.
[6] R. Crandall, "Fast evaluation of Epstein zeta functions" , manuscript, 1998.