List of Student Projects

Transformées en ondelettes par décomposition en B-splines

Raphaël Ertle
Section Systèmes de Communication

January-June 2000

Abstract

The Continuous Wavelet Transform (CWT) is an efficient way to analyze non-stationary signals and to localize and characterize transients. Contrary to the Fourier Transform, wich makes the assumption that the analyzed signal is stationnary and hence gives a global (over time) overview of the frequency spectrum of the signal, the CWT gives a time-frequency description of the signal. The underlying principle of the CWT is to correlate the input signal with a compactly supported motif (the wavelet), which is then dilated by a scale , corresponding to slower versions of the initial wavelet (mother wavelet).

Fast algorithms have been developed to compute it at integer time points and at integer scales, with a complexity of , where represents the size of the input signal. These methods all use recursive schemes.

We propose a new method, based on B-spline expansion of signal and wavelets, that allows its computation at any real scale (wheter integer, rational or anything else), with a complexity of , where represents the size of the input signal.

It outperforms traditional methods based on FFT whose complexity is ), and allows, contrary to other fast methods of complexity to zoom more precisely on desired regions, through finer scale-definition. It also has the big advantage of not presenting a recursive scheme, and is thus well fitted to parallel implementation.

Results

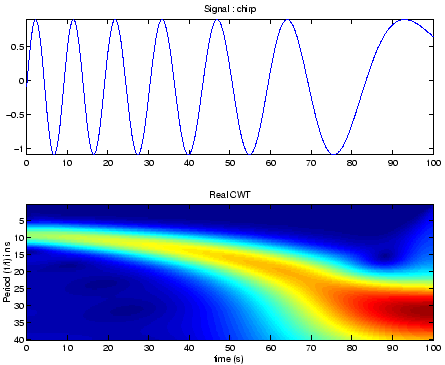
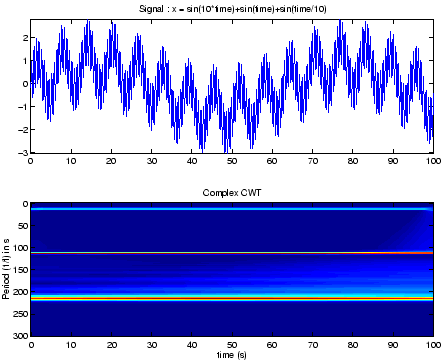
• Perfect signals :

  Figure 1: Input signal : chirp

  Figure 2: Input signal : triple sinusoid

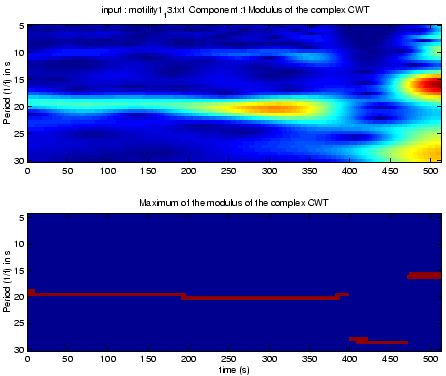
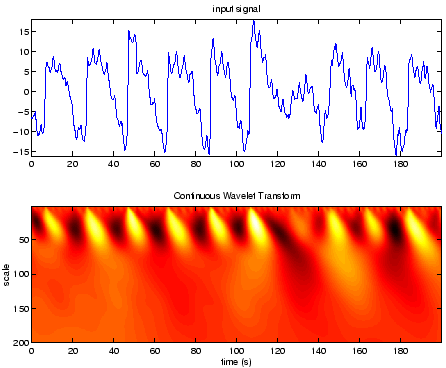
• Biomedical signal :

  Figure 3: Biomedical data (complex CWT)

  Figure 4: Biomedical data (real CWT)