Quincunx Wavelet Transform with Fractional Filters
Asma Jebali
Micro-engineering
Student Project
Semester Project, June 2001
Abstract
The non-separable wavelets may cost much more than the separable ones unless they are implemented in the Fourier domain. We present here a new family of such 2D orthogonal wavelets using a quincunx sampling and a fractional filtering.
For the quincunx downsampling we use a matrix D which turns the inital image by p/4 and reduce it by square root of 2. The upsampling consists on filling the missing blanks by zeros so we keep only the wanted pixels on the quincunx lattice. The chosen matrix leads us to the separable case after each second iteration because D2=2I.
The fractional filtering offers more flexibility: In one hand, the refinement filters are easily tunable thanks to the alpha parameter. In an other hand, we can choose any size of filter since we use them in the frequency domain (FIR, IIR).
The quincunx transform has two advantages with respect to the separable wavelet transform. First, it has less directionnality so the privileged directions are no more the vertical and horizontal ones but rather the diagonal ones. This can be more useful for some applications such as edge detection. Then, it has one more iteration before reducing the image size by 2 so the progression is slower and finer. This can be more determinant for applications like fMRI and so on.
The goal of the project is to implement a fast and efficient algorithm of the quincunx wavelet transform. We implemented this algorithm in Java in order to provide a plugin on ImageJ which is a Java free software of Image Processing. Some results of quincunx image transforms are shown.
Quincunx transform of a grayscale image
Quincunx transform of a RGB image
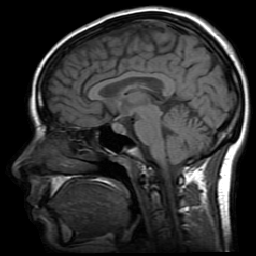
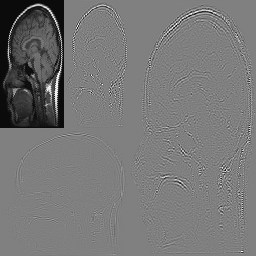
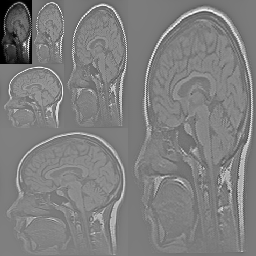
MRI 256x256 32bits
order=p, 3 iterations
order=0.6, 5 iterations
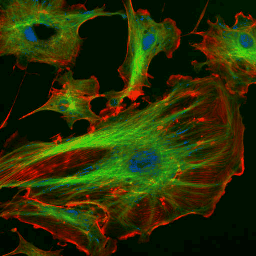
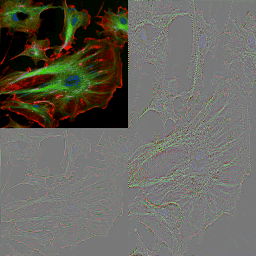
Fluorescent Cells 256x256
order=1.414, 2 iterations
order=0.5, 4 iterations