List of Student Projects

Noise Reduction in Holographic Microscopy Images

Micael Rochat
Microtechnique
Semester Project, Summer 2001

Introduction
Holographic microscopy is a promising method which allows to capture images of living neurons. These images are victims of several noise sources like high vibrations sensibility, CCD coherent noise. Currently, noise reduction is performed by calculating the mean of multiple images.

We implemented noise reduction algorithmes based on the "Independent Model" (IM) and the "Hidden Markov Tree" (HMT) model.IM expresses the independence property of the wavelet Transform; the HMT expresses the persistence property of the Wavelet Transform and the first order hypothesis of "Markov Chains":

  • Independence: The Wavelet Transform decorrelates noise and signal
  • Persistence: the values of coefficients tend to propagate along subbands
  • Markov Hypothesis: p(Si=m|Sr(i)=n1,Sr (r(i))=n2,…) = p(Si=m|Sr (i)=n1)
    where Sr(i) is the parent of Si

Independent Model
A logical idea is to associate a state "S" to every pixel to show the independence property : S=0 Æ "noise" and S=1 Æ "signal".
It implies two probabilities for each state : p(S=0) and p(S=1).
The following image shows that the independence property and the state model lead to a new probability density representation :



Hidden Markov Tree
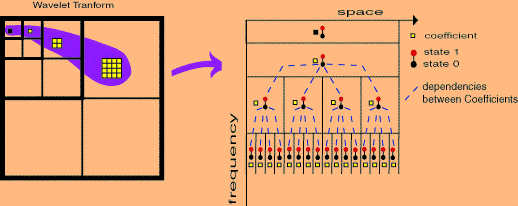
We use the same idea as for the IM algorithm, but we add the persistence property and the Markov Hypothesis. So we obtain a dependance between coefficients as follows:

Each coefficient state depends only on its parent state and not on the parent of its parent (Markov Chain).

Result


Conclusion
IM is a simple intuitiv method. Easy to implement, it gives good results (better than Soft and Hard Threshold)
Both the IM and HMT based algorithms give good results compaired to the Soft and Hard Threshold. Nevertheless, they are subject to numerical instabilities and need a careful initialization.