Image Differentials

An ImageJ plugin that computes the gradient, Laplacian, and Hessian of a grayscale image

Philippe Thévenaz, Biomedical Imaging Group, École polytechnique fédérale de Lausanne (EPFL)

Figure 1. Diatom (left) and its gradient amplitude (right).

• I. Download
• II. Related Work
• III. Explanations
• IV. Operations
• V. Example
• VI. Conditions of Use
• VII. Programmer's Note

I. Download

This distribution is dated September 30, 2024. It includes the complete set of source files, along with the precompiled classes.

• ZIP distribution
• Source file

II. Related Work

This Java class is based on the following paper:
M. Unser, "Splines: A Perfect Fit for Signal and Image Processing," IEEE Signal Processing Magazine, vol. 16, no. 6, pp. 22-38, November 1999.
It is written as a plugin for ImageJ. Please read the ImageJ documentation to learn how to install the plugin.

III. Explanations

This plugin allows you to perform several differentiation operations on images, seen as continuous functions, even though they are stored as discrete pixels. The general principle is to construct the continuously defined function

ƒ(x, y) = ∑_k,l c[k,l] ⋅ φ(x-k, y-l).

Here, we shall concentrate on the specific case where the function

φ(x, y) = β³(x) ⋅ β³(y)

is a tensor-product (separable) cubic B-spline. Then, a typical example of spatial differentiation operation is

∂ƒ(x, y) ⁄ ∂y = ∑_k,l c[k,l] ⋅ β³(x-k) ⋅ ∂β³(y-l) ⁄ ∂y,

where we compute the exact vertical gradient of the continuously defined image.

IV. Operations

Figure 2. Possible operations.

• Gradient Magnitude: the gradient is the first derivative of the image, and is performed along some preferred direction. The result returned by the Gradient Magnitude operation gives the largest gradient magnitude when every possible direction is taken into account. It is a non-negative number computed as

  √( (∂ƒ(x, y) ⁄ ∂x)² + (∂ƒ(x, y) ⁄ ∂y)² ).

• Gradient Direction: the direction of the largest gradient is an angle returned in radians in the range [-π, π]. It is computed as

  arc tan( (∂ƒ(x, y) ⁄ ∂y) ⁄ (∂ƒ(x, y) ⁄ ∂x) ),

  along with considerations on the sign of ∂ƒ(x, y) ⁄ ∂y and of ∂ƒ(x, y) ⁄ ∂x.
• Laplacian: the second derivative can be computed along any orientation and is composed of three terms
  1. ∂²ƒ(x, y) ⁄ ∂x²;
  2. ∂²ƒ(x, y) ⁄ ∂y²;
  3. ∂²ƒ(x, y) ⁄ ∂x∂y.
  The Laplacian operation ignores the third term and returns the average value of the second derivative when taking every orientation into account. It is a signed number computed as

  ∂²ƒ(x, y) ⁄ ∂x² + ∂²ƒ(x, y) ⁄ ∂y².

• Largest Hessian: the computation of the second derivatives of an image yields three terms. While the Laplacian ignores one of them and considers every possible orientation at once, the Hessian takes all three terms into account and is orientation-dependent. The Largest Hessian operation determines the orientation along which the second derivative is maximal. It returns this maximum as a signed number.
• Smallest Hessian: the orientation for which the second derivative is minimal can also be determined. The Smallest Hessian operation returns the minimum of the second derivative as a signed number.
• Hessian Orientation: this operation returns the orientation for which the second derivative is maximal. It is an angle returned in radians in the range [-π ⁄ 2, π ⁄ 2] and corresponds to an orientation without direction. The orientation for the minimal second derivative can be obtained by adding (or subtracting) π ⁄ 2.

V. Example

The following pair of images is typical of the kind of results you can obtain with the present program. The image on the left is the original image, while the image on the right shows its Laplacian.

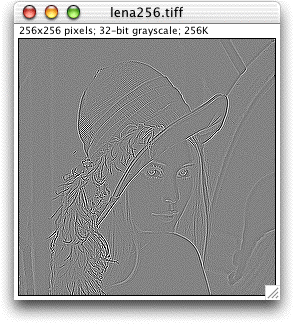Figure 3. Left: 256×256 Lena input image. Right: Resulting Laplacian.

VI. Conditions of Use

This program is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 3 of the License, or (at your option) any later version.

This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.

You should have received a copy of the GNU General Public License along with this program. If not, see https://www.gnu.org/licenses/.

You undertake to include a citation or acknowledgment whenever you present or publish results that are based on this program. EPFL makes no warranties of any kind on this software and shall in no event be liable for damages of any kind in connection with the use and exploitation of this technology.

VII. Programmer's Note

The class Differentials_ contains the five following methods:

These methods have two parameters each and perform the in-place processing of an object of type ImageProcessor, given as first parameter. The only image type that is currently implemented is ImagePlus.GRAY32.

The second parameter is a variable of type double that controls the compromise between speed and accuracy. Its value should be a small positive or null number. The best precision is achieved by setting tolerance = 0.0, at the expense of some (moderate) loss in efficiency. We have observed experimentally that the value that corresponds to the C constant FLT_EPSILON exhibits an excellent trade-off. In Java, this value can be written as Float.intBitsToFloat((int)0x33FFFFFF).