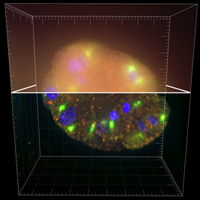
Deconvolution — Making the Most of Fluorescence Microscopy
Deconvolution is one of the most common image-reconstruction tasks that arise in 3D fluorescence microscopy.
The aim of this challenge is to benchmark existing deconvolution algorithms and to stimulate the community to look for novel, global and practical approaches to this problem.
The challenge will be divided into two stages: a training phase and a competition (testing) phase.
It will primarily be based on realistic-looking synthetic data sets representing various sub-cellular structures.
In addition it will rely on a number of common and advanced performance metrics to objectively assess the quality of the results.
Register Now!
PERFORMANCE METRICS
To assess the quality of the reconstruction we provide several scripts
which implement the quality metrics that will be used in the deconvolution
challenge. Below we briefly describe these quality metrics and the usage
of the corresponding MATLAB scripts.
Peak Signal-to-Noise Ratio (PSNR)
The PSNR is defined as
$$
\textrm{PSNR}=10log_{10}(\textrm{peak}^2/\textrm{MSE})
$$
where \(\textrm{peak}\) is the peak value used in the computation and
\(\textrm{MSE}\) is the mean squared error between the reconstruction and the
reference image-stack.
To compute it we provide the
psnr.m script.
Required Input Arguments
- \(x\) : Reconstructed image stack (3D MATLAB array).
- \(f\) : Ground-truth image stack (3D MATLAB array).
Optional Input Arguments
- \(p\) : Peak value used in the computation of PSNR (Default: maximum value of \(f\)).
Output Arguments
- \(\textrm{psnr}\) : Peak signal to noise ratio.
- \(\textrm{mse}\) : Minimum mean squared error between \(x\) and \(f\).
Normalized Mean Integrated Squared Error (NMISE)
We use a modified version of the original NMISE metric, which is better
suited to the image restoration problem. It is defined as
$$
\textrm{NMISE}=\frac{1}{N}\sum_{i=1}^N(x_i - f_i)^2/{f_b}_i.
$$
To compute it we provide the
nmisec.m script.
Required Input Arguments
- \(x\) : Reconstructed image stack (3D MATLAB array).
- \(f\) : Ground-truth image stack (3D MATLAB array).
- \(f_b\) : Intermediate result, \(f_b=\mathbf{A}\mathbf{x}+\mathbf{b}\), of the observation model (3D MATLAB array). Output of the
ForwardModel3D.m script.
Output Arguments
- \(\textrm{nmise}\) : Normalized mean integrated squared error between \(x\) and \(f\).
Structure Similarity Index (SSIM)
The structural similarity (SSIM) index is a metric for measuring the
similarity between two images. A description of this metric can be found
on
Wikipedia.
To serve the needs of the 3D reconstruction we provide the
ssim3D.m
script which can be applied to image volumes.
Required Input Arguments
- \(x\) : Reconstructed image stack (3D MATLAB array).
- \(f\) : Ground-truth image stack (3D MATLAB array).
Optional Input Arguments
- \(K\) : constants in the SSIM index formula (see ssim_index.m) (Default : \(K\) = [0.01 0.03]).
- \(\textrm{window}\) : local window for statistics (see ssim_index.m). The default window is Gaussian given by
window = fspecial('gaussian', 11, 1.5).
- L : dynamic range of the images (Default: maximum value of \(f\)).
Output Arguments
- \(E\) : The mean ssim index over all the slices of the image stacks.
- \(M\) : The minimum ssim index over all the slices of the image stacks.
Fourier Shell Correlation
The Fourier shell correlation measures the normalized cross-correlation coefficient between two image stacks over corresponding shells in the Fourier space, and is defined as
$$ \mbox{FSC}\left( r \right)=\frac{\sum_{r_i\in r}\hat{f}_1(r_i)\cdot \hat{f}_2^*(r_i)}{\sqrt{\sum_{r_i\in r}{|\hat{f}_1(r_i)|}^2\cdot\sum_{r_i\in r}{|\hat{f}_2(r_i)|}^2}}, $$
where \(\hat{f}_1(r_i), \hat{f}_2(r_i)\) are the Fourier components of the two image stacks at the given spatial frequency \(r_i\). To compute it we provide the
FourierShellCorrelation.m script.
Required Input Arguments
- m : Output of the
FourierMetricsConstructor.m script.
- \(\hat{f}_1\) : The Fourier transform of the reconstructed image stack.
- \(\hat{f}_2\) : The Fourier transform of the ground-truth image stack.
Output Arguments
- \(\mbox{FSC}\) : The Fourier shell correlation as defined above.
Relative Energy Regain
The relative energy regain is a Fourier-based quality metric which measures the recovery of information at a range of absolute spatial frequency. For more informations about this metric we refer to the following article: Heintzmann. Estimating missing information by maximum likelihood deconvolution. Micron 38 (2007) 136-144.
To compute it we provide the
RelativeEnergyRegain.m script.
Required Input Arguments
- m : Output of the
FourierMetricsConstructor.m script.
- \(\tilde{I}\) : The Fourier transform of the reconstructed image stack.
- \(\tilde{O}\) : The Fourier transform of the ground-truth image stack.
Output Arguments
- \(\mbox{G}_R\) : The relative energy regain.
Important Dates
Deadline for submission
The registered participants will receive soon a personalized upload link.
January 6, 2014
Beginning of evaluation stage
The evaluation stage of the second edition of the challenge has started.
November 6, 2013
Evaluation stage
The official stage of the challenge will last around 2 months.
November/December, 2013
Beginning of training stage
The training stage of the second edition of the challenge has started. Follow this link to register and receive e-mail updates.
July 17, 2013