Abstract

The Laboratory of Robotics Systems (LSRO) has developed two high precision robots of 3 and 6 degrees of freedom. In order to calibrate the systems, a large amount of input-output pairs have been measured. Input: position of the motors, Output: position of the end-effector. At these "training points" the input-output relation is now known exactly. At all other points the relation is found by interpolation (or, in the case of noisy measurements, by approximation).
We approached the problem from a theoretical point of view and considered the general case of non-uniform sampling in m dimensions, where the solution can be expressed through radial basis functions (RBF). For the case of uniform sampling we derived a solution for the approximation and the interpolation problem expressed in the basis of cubic B-splines. In contrast to radial basis functions, B-spines have the advantage of a finite support which allows fast reconstruction.

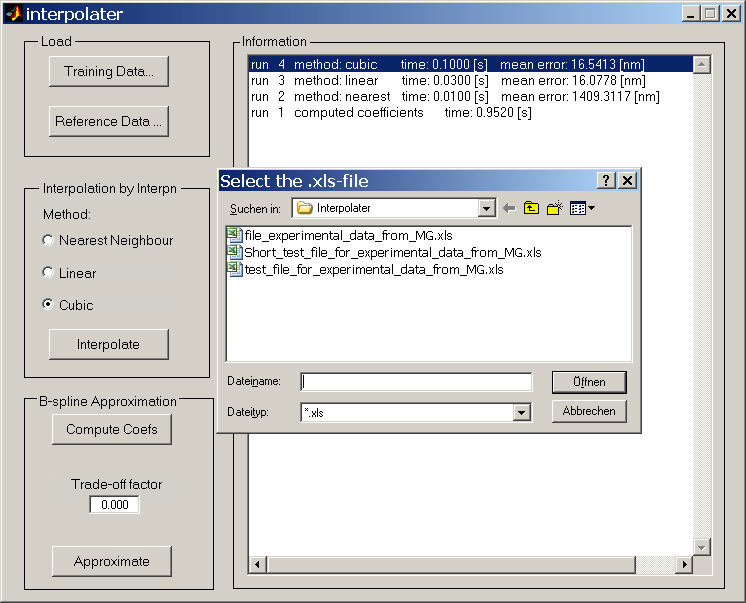
Three algorithms have been implemented in MATLAB:

• multi-dimensional interpolation based on the existing MATLAB function "interpn"
• three-dimensional interpolation and approximation for non-uniform sampling based on radial basis functions
• multi-dimensional interpolation and approximation based on cubic B-splines

The LSRO has provided two experimental data sets of the "Delta Cube" robot. The first set of 15^3 training points was used to compute the RBF and B-spline coefficients. The second set of 10^3 reference points was then used to validate the proposed algorithms. All three algorithms produced good results. The goal of errors below 100 nm has been surpassed with errors around 17 nm. It has also been shown, that better results can be achieved if interpolation is replaced by approximation (accuracy improvement of roughly 10%). A graphical user interface has been created in order to facilitate further experiments.