 |
 |
 |
 |
 |
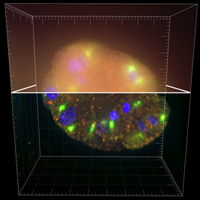
Deconvolution is one of the most common image-reconstruction tasks that arise in 3D fluorescence microscopy. The aim of this challenge is to benchmark existing deconvolution algorithms and to stimulate the community to look for novel, global and practical approaches to this problem.
The challenge will be divided into two stages: a training phase and a competition (testing) phase. It will primarily be based on realistic-looking synthetic data sets representing various sub-cellular structures. In addition it will rely on a number of common and advanced performance metrics to objectively assess the quality of the results.
The central part of the forward model is a discrete convolution of the form $$ (f*h)[\boldsymbol{n}] = \sum_{\boldsymbol{k} \in \ \mathbb{Z}^3} f[\boldsymbol{k}] \, h[\boldsymbol{n} - \boldsymbol{k}], $$ where \(f\) represents the ground-truth distribution of fluorophores and \(h\) represents the point-spread function (PSF).
Unlike standard formulations of deconvolution, we do not use periodic boundary conditions. Instead we will exploit the following facts.
The complete forward model is given by $$ g[\boldsymbol{n}] \sim Q\bigg(\mathcal{P}\Big((A\{f\})[\boldsymbol{n}] + b\Big) + w[\boldsymbol{n}]\bigg). $$ Here, \(A\) is a linear operator which includes the convolution operation, the constant \(b\) corresponds to a background signal, and the notation \(\mathcal{P}(\lambda)\) represents a Poisson random variable of intensity \(\lambda\). The latter models shot noise, which is due to the quantum nature of light. The symbols \(w[\boldsymbol{n}] \sim \mathcal{N}(0, \sigma^2)\) denote IID Gaussian random variables corresponding to detector noise. Finally \(Q\) is a quantization operator defined by $$ Q(x) = \begin{cases} \arg\min_{n \in \mathbb{N}} |x - n| & \text{if } x > 0, \\ 0 & \text{otherwise} \end{cases} $$ and \(g\) represents the measured data. Note that our model is based on the simplifying assumption of a photon-counting detector. Thus it does not involve a gain parameter and the measurements \(g[\boldsymbol{n}]\) can directly be interpreted in terms of photons.
The convolution product \(h*f\) can be represented in matrix form as \(\mathbf{Hf}\), where the vector \(\mathbf{f}\) contains the samples \(f[\boldsymbol{n}]\) in lexicographic order and \(\mathbf{H}\) is a block-circulant matrix constructed from the samples \(h[\boldsymbol{n}]\). This is also one of the most common deconvolution settings used in the literature.
Despite the popularity of using a circulant operator in the deconvolution setting, such a choice implies periodic boundary conditions for the object of interest. This particular assumption is quite unrealistic and, for real data, often leads to severe artefacts in the reconstuction. In this challenge, we provide a forward model that serves as a better approximation of the process taking place in the microscope. Instead of assuming specific boundary conditions, we explicitly state our lack of information outside the boundary of the image. Mathematically speaking, the employed forward operator, \(\mathbf{A}\), can be described as the composition of the following operations: $$\mathbf{A}\mathbf{f}=(\mathbf{M}\mathbf{H}\mathbf{Z})\mathbf{f}.$$ where \(\mathbf{H}\) is a circulant convolution matrix that admits a fast FFT implementation and \(\mathbf{M}\) and \(\mathbf{Z}\) are suitable masking operators. Specifically, \(\mathbf{M}\) is a masking operator which returns only the part of the circulant convolution that is valid. This means that the operator \(\mathbf{M}\) truncates those parts of the linear convolution which are computed based on the periodic boundary assumption. In particular, for an object \(f\) of size \([N_x,\, N_y,\, N_z]\) and a PSF \(h\) of size \([L_x,\, L_y,\, L_z]\), the size of the valid part of the linear convolution is equal to \([N_x-L_x+1,\, N_y-L_y+1,\, N_z-L_z+1]\). This is always true if we assume that the support of \(f\) is larger than that of \(h\) in all dimensions.
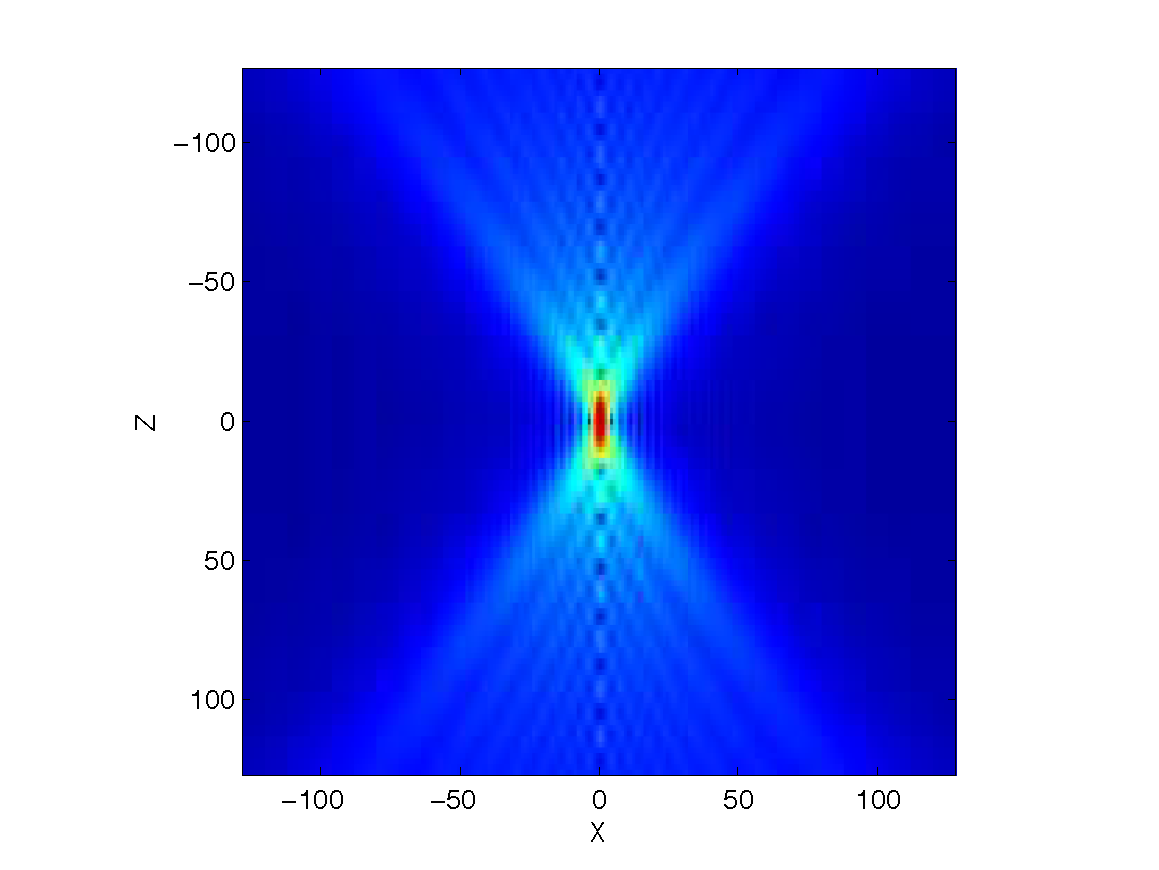
As it was mentioned above, biological samples are typically thin while the effect of the PSF
on the measurements is larger in the axial direction than in the
lateral one (see Fig. 1). Thus, it is reasonable to use a PSF whose support
in the axial direction is broader than the support of the object at the same direction. These two facts combined
suggest that the convolution in the Z-dimension must be performed so that the roles
of the object and the PSF are interchanged. Therefore, for an object \(f\) of size \([N_x,\, N_y,\, N_z]\) and
a PSF \(h\) of size \([L_x,\, L_y,\, L_z]\) where \(L_z > N_z\), the forward operation, \(\mathbf{A}\mathbf{f}\), results to a measured object of size \([N_x-L_x+1,\, N_y-L_y+1,\, L_z-N_z+1]\).
This outcome is achieved by using the linear operator \(\mathbf{Z}\), which
zeropads the object \(f\) in the axial direction so that its size becomes equal to \(2L_z-N_z\).
For more details, we refer the participants to the documentation of the Matlab scripts as well as to
the distributed code of the challenge where computationally efficient implementations of the forward operator \(\mathbf{A}\) (Direct.m) and of its adjoint \(\mathbf{A}^T\) (Adjoint.m) are made available.
[2]. S. F. Gibson and F. Lanni. Experimental test of an analytical model of aberration in an oil-immersion objective lens used in three-dimensional light microscopy. Journal of the Optical Society of America A, 9(1):154-166, 1992.↩
The registered participants will receive soon a personalized upload link.
January 6, 2014The evaluation stage of the second edition of the challenge has started.
November 6, 2013The official stage of the challenge will last around 2 months.
November/December, 2013The training stage of the second edition of the challenge has started. Follow this link to register and receive e-mail updates.
July 17, 2013