| CONTENTS |
| MONOGENIC |
|
Download Plugin for ImageJ [Version 21.09.2009] |
The software package MonogenicJ performs multiresolution monogenic analyses of 2D images. It extracts wavelet-domain features that characterize the local orientation, the phase and the dominant frequency of an image patch at various levels of resolution. The package is available for download as a Java plugin for ImageJ.

| Zoneplate | (10/10) | Feature: Color Survey | (11/12) | |||
 |
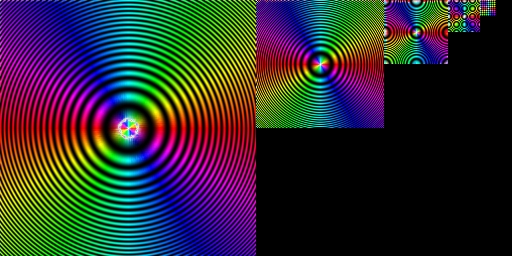 |
|||||
| « Previous • Next » | « Previous • Next » | |||||
Experiment: scaled values, J=5, σ=1
H: Orientation S:Coherency B:Input
MonogenicJ has the ability to compute and display Riesz and Laplace wavelet components, structure-tensor descriptors, and monogenic features in a dyadic multiresolution framework. It offers two modes of analysis:
The Riesz-Laplace wavelet analysis decomposition provides three multiscale monogenic components:
These are used to build the tensor matrix J which is used to extract the following image descriptors:
Note that the tensor matrix is computed for each wavelet cell using a local averaging scheme (Gaussian window).
The next step is the wavelet-domain monogenic analysis which is equivalent to performing a 1D analytic signal analysis along the dominant orientation. This is achieved via a steering mechanism and leads to the extraction of the following local features.
The complete technical details together with some examples of applications are given in the publication below.
M. Unser, D. Sage, D. Van De Ville, "Multiresolution Monogenic Signal Analysis Using the Riesz-Laplace Wavelet Transform," IEEE Transactions on Image Processing, vol. 18, no. 11, pp. 2402-2418, November 2009.
Free and easy-to-use software
The software is a plugin for ImageJ, a general purpose image-processing package. ImageJ has a public domain licence; it runs on several plateforms: Unix, Linux, Windows, Mac OSX.
Quick installation
The whole process should not take more than a couple of minutes.
How to perform the monogenic analysis of an image
Display of the features
Screenshot
© 2022 EPFL • webmaster.big@epfl.ch • 11.08.2022