Implementation of fractional splines filters for wavelet transforms

Fractional splines are a new type of splines that have been studied in the group. They are similar to traditional B-splines, except that they depend upon a continuous (fractional) parameter and not a discrete order like traditional ones. However, these splines are not compactly supported, so that the calculus needed to obtain the filters required for wavelet transforms get more complicated.

Since we would like to interest people into experimenting with wavelets using such splines, it is necessary to craft a code to generate the corresponding filters.

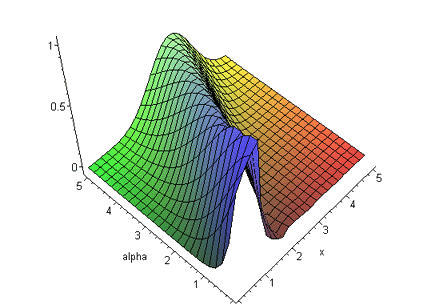
Fig. 1 Fractional splines

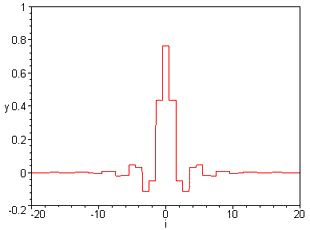
Fig. 2 Filter for fractional spline of order P

The filters are built by calculating them in the fourier domain and performing a FFT. The process involves calculating an infinite sum, whose convergence has been mathematically accelerated to improve the performance of the code. The filters have been characterised and empirical rules for the optimal filter length have been deduced.

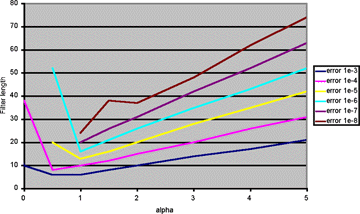
Fig. 3 Empirical rules for optimal filter length

The code written is ready to be used by other people and can easily be integrated in existing code that performs wavelet transforms. This way, people may experiment with these wavelets and maybe some applications will be found.

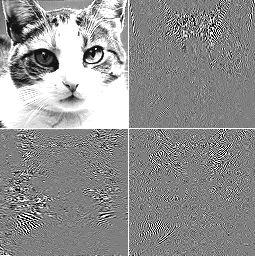
Fig. 4 Wavelet transform of a cat using fractional B-splines of order P