Author: Olivier Bernard
Olivier Bernard is currently an Associate Professor at INSA (Lyon - France) and a member of the CREATIS-LRMN Laboratory (CNRS 5220, INSERM U630, INSA, Claude Bernard Lyon 1 University).
We present here a new formulation of level-set where the implicit function is modelled as a continuous parametric function expressed on a B-spline basis. Starting from the level-set energy functional, this formulation allows computing the solution as a restriction of the variational problem on the space spanned by the B-splines. As a consequence, the minimization of the functional is directly obtained in terms of the B-splines parameters. We also show that each step of this minimization may be expressed through a separable convolution operation, which yields a very efficient algorithm. As a further consequence, each step of the level-set evolution may be interpreted as a filtering operation with a B-spline kernel. Such filtering induces an intrinsic smoothing in the algorithm, which can explicitly be controlled via the degree and the scale of the chosen B-spline kernel.
O. Bernard, D. Friboulet, P. Thevenaz and M. Unser "Variational B-spline level-set: a linear filtering approach for fast deformable model evolution," Submitted to IEEE transactions on Image Processing, 2007
Demonstration
|
How to use
|
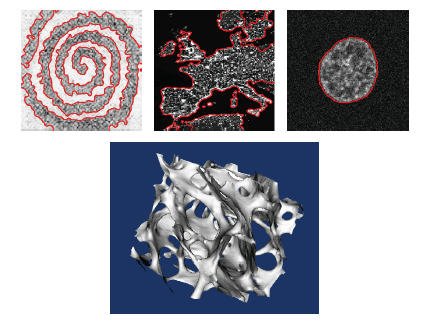
The behaviour of this approach is illustrated on simulated images as well as experimental images from various fields. The segmentation experiments are based on the Chan-Vese functional, which aims at partitioning the image into regions with piecewise constant intensity. The following settings are applied to all experiments:
The influence of two parameters of the method are illustrated in this demonstration: a parameter nu which weights the curvature term in the functional, and a parameter h which controls the smoothing of the solution via the scale of the B-splines. We indicate the number of iterations needed to reach the final solution. A segmentation obtained through a simple binary threshold is used for comparison purposes
We give in the proposed paper a description of the results obtained for the images named: Spirale, donuts-Noisy-25dB, donuts-Noisy-20dB, donuts-Noisy-15dB, Yeast and Europe-Night-Lights.