Wavelet-based methods for the solution of inverse problems and de-noising

Matthieu Guerquin-Kern	Master Project
Département EEA, Ecole normale supérieure de Cachan	August 2007

Inverse problem are challenging due to the presence of noise.

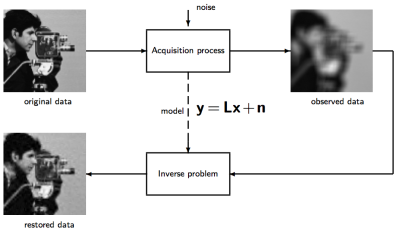
In order to solve such an inverse problem we could use a variational approach, that is, the solution could be expressed as the minimization of a functional. This functional typically consists of a fidelity and a regularization term (assuming that the solution is rather regular). Recently developed algorithms have a regularity term that consists of wavelet coefficients [1] [2] [3].

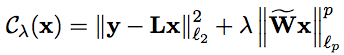
Daubechies et al. proposed an iterative algorithm for orthonormal wavelet bases with two simple steps. The goal of my work was to design a de-noising algorithm using semi-orthogonal wavelet bases.

First, we devised a computationally-efficient method for the de-noising problems. We ensured the convergence for semi-orthogonal wavelet bases. Moreover, we proved that it can easily be extended to every linear inverse problem.

Finally, we implemented the algorithm and studied the impact of each parameter. We used the semi-orthogonal fractional-spline wavelet transform [4], and observed, in particular the importance of pre and post-filtering.

De-noising Example

Main references

I. Daubechies, M. Defrise, and C. De Mol. An iterative thresholding algorithm for linear inverse problems with a sparsity constraint. Communications on Pure and Applied Mathematics, 57(11):1413-1457, August 2004.
M. A. T. Figueiredo and R. D. Nowak. An EM algorithm for wavelet-based image restoration. IEEE Transactions on Image Processing, 12(8):906-916, August 2003.
J. Bect, L. Blanc-Féraud, G. Aubert, and A. Chambolle. A l1-unified variational framework for image restoration. Lecture Notes in Computer Science, 3024:1-13, 2004.
M. Unser and T. Blu. Fractional splines and wavelets. SIAM Review, 42(1):43-67, March 2000.