3D Microscopy Deconvolution on GPU

Sander Kromwijk

Semester Project

Section of Computer Science, EPFL

January 2014

Abstract

The goal of this project is to take the deconvolution algorithms described in [1] and [2], and transfer them to the GPU to reduce processing time.

In biomedical research, microscopes used close to their limits exhibit heavy artefacts in the resulting image. Before the image can be used and interpreted, it needs to be processed to remove noise and reverse the microscope's convolution kernel. This is a very computationally expensive operation; every image takes a long time to compute. The algorithm presented in [1] and [2] (and variational methods in general) also need tuning of certain parameters, requiring a recomputation of the whole image at each try. By decreasing processing time, this is made more convenient, and less time-consuming.

[1] S. Lefkimmiatis and M. Unser, "Poisson image reconstruction with hessian schatten-norm regularization," 2013.
[2] S. Lefkimmiatis, J.Ward, and M. Unser, "A hessian schatten-norm regularization approach for solving linear inverse problems," 2013.

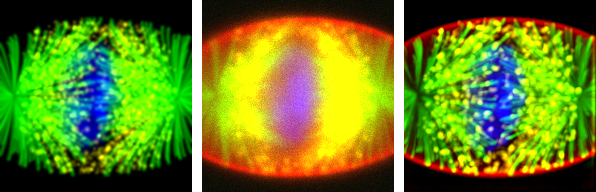
Sample results

Figure 1: Sample deconvolution results. From left to right, Z max-projection of the Ground Truth, Simulated observation, and result of deconvolution. Note: the ground truth doesn't contain the red channel, as it would hide/obfuscate the other channels. It is a uniformly colored ellipsoid covering the whole cell.

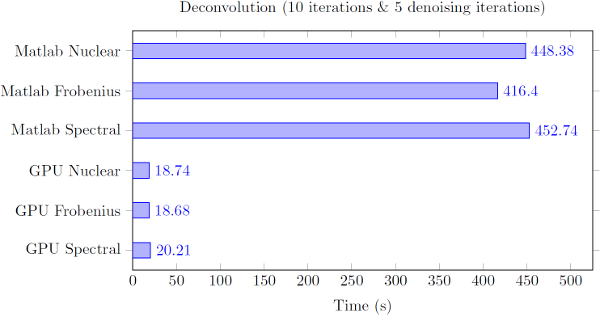
Result graph

Figure 2: Time to deconvolve a 320x320x192 image with Poisson noise using various norms.