| Biomedical Imaging Group |
| CONTENTS | ||||||||
|---|---|---|---|---|---|---|---|---|
| Home Page | ||||||||
| News & Events | ||||||||
| Members | ||||||||
| Publications | ||||||||
| Tutorials and Reviews | ||||||||
| Research | ||||||||
| Demos | ||||||||
| Download Algorithms | ||||||||
| BEEPS | ||||||||
|
| DOWNLOAD |
|---|
| UNIX distribution |
| Macintosh distribution |
| PC distribution |
Bi-Exponential Edge-Preserving Smoother
An ImageJ plugin that smoothes an image without altering its edges.
Philippe Thévenaz, Biomedical Imaging Group, Swiss Federal Institute of Technology Lausanne

Figure 1. Original.

Figure 2. A smoothed image with preserved edges takes a cartoonish appearance.
General Description
The smoothing is applied by the way of a bi-exponential filter, itself realized by a pair of one-tap recursions. It is therefore very fast; moreover, its computational cost is truly independent of the amount of smoothing. Meanwhile, the preservation of edges is obtained by a range filter akin to the range filter found in a bilateral filter. More technical details are available here.
The plugin allows one to control the amount of smoothing, the type of range filter, its broadness, and to iterate the filter several times if desired. We illustrate in Figure 2 a possible outcome of this filter. Here, we iterated the BEEPS 10 times with a Gaussian range filter, σ = 10, and the spatial decay λ = 0.1.
I. Download
This distribution is dated September 9, 2011. It includes the source files, along with a jar file that contains the precompiled classes.
- UNIX distribution [51,712 bytes]
- Macintosh distribution [39,493 bytes]
- PC distribution [22,332 bytes]
II. Related Work
This set of Java classes is based on the following paper:
P. Thévenaz, D. Sage, M. Unser, "Bi-Exponential Edge-Preserving Smoother," IEEE Transactions on Image Processing, in press. Other relevant on-line publications are available at http://bigwww.epfl.ch/publications/.
BEEPS has been written as a plugin for ImageJ. Please read the ImageJ documentation to learn how to install plugins.
III. Technical Explanations
The bi-exponential edge-preserving smoother (BEEPS) is an image-processing filter that transforms an input image into an output image of the same size. The goal of the BEEPS is to iron out irrelevant details of the image without compromising strong edges. Thus, its effect is similar to that of a bilateral filter, except that the BEEPS is much faster than the bilateral filter. It is controlled by tuning a so-called range filter, along with the amount of spatial smoothing.
In this plugin, the range filter is either Gaussian-like or sech-like. (The sech function is the usual hyperbolic secant). In both cases, the contribution of the range filter is controlled by its standard deviation: a large standard deviation corresponds to a broad range filter that has a weak effect and allows for the smoothing of all but the strongest edges; a small standard deviation corresponds to a narrow range filter that has a strong effect and forbids the smoothing of most edges.
The amount of spatial smoothing is controlled by the decay of a bi-exponential filter. Useful decays belong to the interval [0, 1). When the decay is slow (near 0), the filter has a long-range reach and the spatial smoothing is strong. When the decay is fast (near 1), the filtering is localized and the spatial smoothing is weak. Please note that the decay λ that controls this plugin corresponds to (1 − λ) in the associated publication.
IV. User Manual
The plugin requests at least one open image at launch. All image types are accepted, except RGB Color and 8-bitColor. In the case of a RGB Stack or a HSB Stack, the processing will be performed independently on all channels.
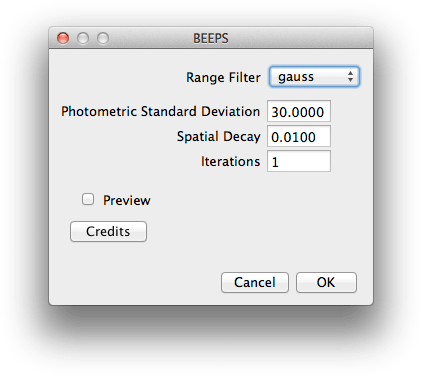
Figure 3. Initial dialog.
At launch, a dialog window will appear (see Figure 3). The role of its various components is as follows:
- Range Filter: Selection of the type of range filter. The choice "gauss" corresponds to the function s(u, v) = exp(−(u − v)2 ∕ (2 σ2)). The choice "sech" corresponds to the choice s(u, v) = sech(π (u − v) ∕ (2 σ)).
- Photometric Standard Deviation: Broadness of the range filter. The number provided is the value of the variable σ in the formulæ of the range filter.
- Spatial Decay: Decay of the impulse response of the spatial filter. The impulse response of the filter is h[k] = (λ ∕ (2 − λ)) (1 − λ)|k|. The number provided is the value of the variable λ. Please note that λ in this plugin is a decay, while λ in the associated publication is a contra-decay.
- Iterations: Number of iterative applications of the BEEPS. A value 1 means that the filter is applied just once—it does not imply that there would be one additional iteration beyond the initial application.
- Preview: When ticked, provides a preview of the effect of the filter. The type of range filter is always "gauss" for this preview.
- Credits: Brings a text panel that documents the plugin and provides the legal notice.
V. Conditions of Use
© 2011 Philippe Thévenaz
This program is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 3 of the License, or (at your option) any later version.
This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.
You should have received a copy of the GNU General Public License along with this program. If not, see https://www.gnu.org/licenses/.
You undertake to include a citation or acknowledgment whenever you present or publish results that are based on this program. EPFL makes no warranties of any kind on this software and shall in no event be liable for damages of any kind in connection with the use and exploitation of this technology.
