| SURE/PURE-LET Denoising of Multidimensionnal Fluorescence Microscopy Data |
Investigators: Florian Luisier, Cédric Vonesch |
|
Summary:
We propose fast and efficient wavelet-based algorithms for denoising multidimensional fluorescence data. Our approach relies on:
- the minimization of an unbiased estimate of the mean-squared error between the original (unknown) data and the processed one, which solely depends on the observed noisy data.
- the description of the denoising process as a linear combination of non-linear processing.
|
|
In image analysis, the extraction of information can be significantly altered by the presence of random distortions called noise. Nowadays, the measurements can be acquired with various imaging modalities, such as CT, PET, MRI, fluorescence microscopy,... In all these techniques, the contaminating noise usually contains a signal-dependent part (e.g. fluctuations of the number of photons hitting the detectors) and a signal-independent component (e.g. intrinsic thermal and electronic variations of the acquisition devices). In many applications of biomedical imaging, the first step thus consists in reducing the level of the overall noise, without degrading the key image features.
|
|
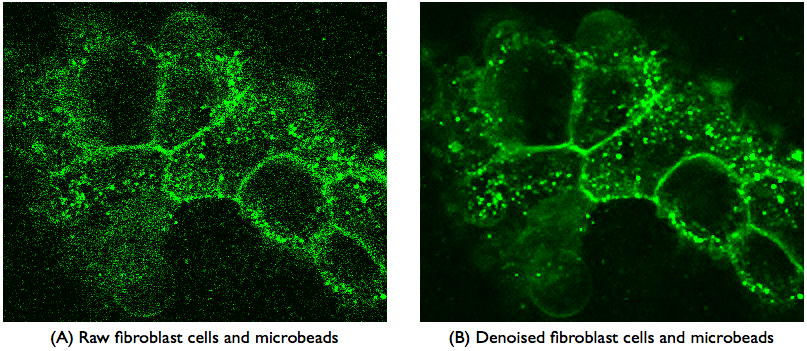 |
Our main contribution is the revitalization of an under-exploited statistical tool and its application to the image restoration problem. The foundation of our approach goes back to the work of Charles M. Stein, a statistician who gave an unbiased estimate of the risk of an essentially arbitrary estimate of the mean of a multivariate normal distribution. His result is nowadays known as the SURE theory. The Gaussianity of the distribution is the key hypothesis of SURE.
In the first part of our work, we reformulate the calculations of Stein to give an explicit unbiased estimation of the MSE (for an arbitrary transformed-domain processing) which only depends on the noisy data. We present a new form of wavelet estimator which is described by a linear expansion of thresholds (LET). By taking advantage of the quadratic form of the MSE estimate, we show that the search for the optimal parameters of the linear combination of elementary thresholds boils down to the solution of a linear system of equations. The key novelty of our approach is that it does not involve any prior statistical modeling of the noise-free wavelet coefficients -we do not even consider them as a random process- contrary to what is commonly done in the image denoising community.
In the second part of our research, we show that the SURE theory can be extended beyond the restricted case of additive Gaussian noise. In particular, we give an explicit expression of an unbiased estimate of the MSE (coined PURE) for a Poisson process embedded in additive Gaussian noise. This observation model is particularly well-suited to characterize fluorescence microscopy data.
|
|
Collaborations: Thierry Blu, Michael Unser |
|
|
Funding: This work is supported by the Center for Biomedical Imaging (CIBM) of the Geneva-Lausanne Universities and the EPFL, the foundations Leenaards and Louis-Jeantet, the Swiss National Science Foundation under grant 200020-109415, as well as by a Direct Grant #2050420 from the Hong Kong Research Grants Council. |
|
|
[2] | F. Luisier, C. Vonesch, T. Blu, M. Unser, "Fast Haar-Wavelet Denoising of Multidimensional Fluorescence Microscopy Data," Proceedings of the Sixth IEEE International Symposium on Biomedical Imaging: From Nano to Macro (ISBI'09), Boston MA, USA, June 28-July 1, 2009, pp. 310-313.
|
[3] | S. Delpretti, F. Luisier, S. Ramani, T. Blu, M. Unser, "Multiframe SURE-Let Denoising of Timelapse Fluorescence Microscopy Images," Proceedings of the Fifth IEEE International Symposium on Biomedical Imaging: From Nano to Macro (ISBI'08), Paris, France, May 14-17, 2008, pp. 149-152.
|
|
|
|
