SPM versus WSPM: Sensitivity and Specificity for Multi-Session fMRI Data

D. Van De Ville, M. Seghier, F. Lazeyras, M. Pelizzone, T. Blu, M. Unser

Invited talk, Proceedings of the Twelfth Annual Meeting of the Organization for Human Brain Mapping (HBM'06), Firenze, Italian Republic, June 11-15, 2006, pp. S94.

Wavelet-based statistical parametric mapping (WSPM) combines powerful denoising in the wavelet domain with statistical testing in the spatial domain. It guarantees strong type I error control and thus high confidence in the detections. In this poster, we propose a comparison of WSPM and SPM2, based on the results of multi-session experimental data.

The general linear model (GLM) setup was done using SPM, including regressors from the realignment procedure and the autoregressive model for serial correlations. For each session, functional maps of the combined contrast (all frequencies-rest) were obtained for a broad range of significance levels with SPM (4mm smoothing) and WSPM (orthogonal B-spline wavelets slice-by-slice; degree 1.0; 2 iterations; combination of 4 spatial shifts). SPM compensates for multiple testing using the Gaussian Random Field theory, while WSPM uses simple Bonferroni correction. The results were then analyzed using two different criteria:

1. Empirical: we report the number of activated voxels inside/outside a manually defined region of interest (ROI) around the auditory cortex, as shown in Fig. 1.
2. Theoretical: we analyze the detection maps of the 4 sessions using the non-parametric approach of Genovese (1997). This method allows us to estimate the sensitivity and specificity by using a binomial mixture model, and thus to obtain a receiver-operating-curve (ROC).

Figure 1.

In Fig. 2, we show for each session the number of detections for SPM and WSPM, inside and outside the ROI, as a function of the significance level. Notice that the significance level is at the volume level; i.e., α = 1.0 corresponds to the expectation of a single false positive for the whole volume. We found that both methods are about equally calibrated for α = 1.0. However, the slope of the curve that links the number of detections as a function of the significance level is lower for WSPM than for SPM, which means more detections with WSPM for the same type I error probability. Interestingly, number of detections outside the ROI is not higher for WSPM, suggesting that its higher sensitivity does not lead to false positives augmentation.

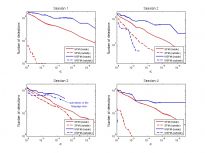
Figure 2.

In Fig. 3, we show the ROCs after estimating the binomial mixture model for both methods. The mixture parameter is globally estimated. The higher performance of WSPM is confirmed: higher sensitivity (more true positives) combined with higher specificity (more true negatives).

Figure 3.

In Fig. 4, we show the area under the ROC (i.e., sensitivity times specificity), which is a good single measure for the performance of the detection technique. This figure illustrates again the excellent balance of sensitivity and specificity for WSPM.

Figure 4.

Finally, we note that WSPM guarantees its strong type I error control using conservative assumptions only.

References

1. C.R. Genovese, D.C. Noll, W.F. Eddy, "Estimating Test-Retest Reliability in Functional MR Imaging I: Statistical Methodology," Magnetic Resonance in Medicine, vol. 38, no. 3, pp. 497-507, September 1997.

2. D. Van De Ville, T. Blu, M. Unser, "Integrated Wavelet Processing and Spatial Statistical Testing of fMRI Data," NeuroImage, vol. 23, no. 4, pp. 1472-1485, December 2004.

@INPROCEEDINGS(http://bigwww.epfl.ch/publications/vandeville0604.html,
AUTHOR="Van De Ville, D. and Seghier, M. and Lazeyras, F. and Pelizzone,
	M. and Blu, T. and Unser, M.",
TITLE="{SPM} {\textit{versus}} {WSPM}: {S}ensitivity and Specificity for
	Multi-Session {fMRI} Data",
BOOKTITLE="Twelfth Annual Meeting of the Organization for Human Brain
	Mapping ({HBM'06})",
YEAR="2006",
editor="",
volume="",
series="",
pages="S94",
address="Firenze, Italian Republic",
month="June 11-15,",
organization="",
publisher="",
note="Invited talk")