Fractional Splines and Wavelets have proven to be adequate bases for signal and image analysis, since they are adaptable in smoothness and decay. By introducing a new parameter it is possible to construct complex splines. They still generate multiresolution analyses and thus allow the construction of complex wavelet bases.

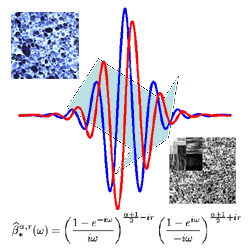
Since these bases consist in complex-valued functions, they provide phase information. Phase can be used for image analysis algorithms and yields stability for a series image processing methods.

This projects consists in providing an ImageJ plugin that performes the complex spline wavelet transform. The implementation shall be based on the Fourier transform to exploit the simple form of complex splines and wavelets in frequency domain. Moreover, the complex spline wavelet transform can be easily extended to multi-dimensions, as well as to a redundant transform.

The algorithm and the performance of the complex wavelets may be tested on real images. Then the comparision of real and complex wavelets, of the redundant with the non-redundant may be evaluated in applications such as denoising, edge detection or fusion of microscopic images.

For further reading see Fractional Splines.