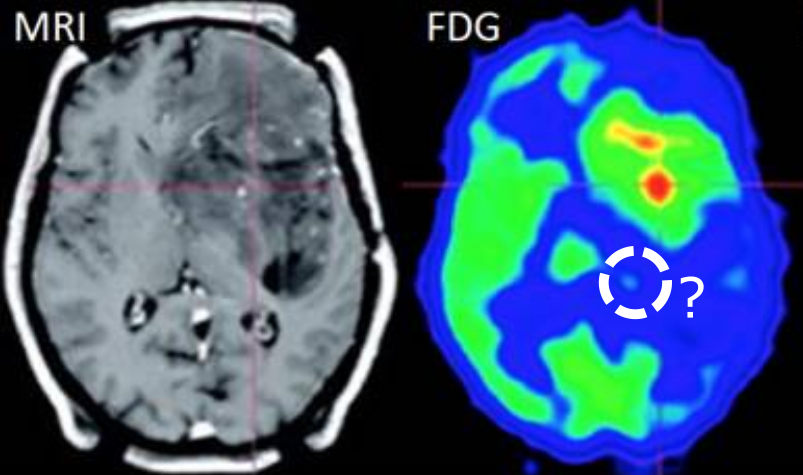
Be it through a variational framework or using neural networks, most reconstruction algorithms in biomedical imaging (CT, MRI, TFM, etc.) are deterministic and thus output a single image. To better account for the propagation of acquisition noise, Bayesian approaches exploit the equivalence between regularisation and statical priors to provide a full posterior distribution of the image. Rather than a single estimate, the posterior describes the relative likelihood of the entire image space. In this context, the deterministic estimate corresponds to the image of maximum probability (MAP) in the Bayesian posterior. However, the resulting probability distributions are seldom used to further investigate the image in medical terms. For example, one could ask whether a salient spot – say a potential tumour – is statistically significant to the reconstruction of the entire image or is instead the result of amplifying acquisition noise. Especially in the case of non-linear priors, the hypothesis tests corresponding to these questions would be very expensive to compute. In this project, we will explore how to estimate the posterior-weighted integrals necessary to the formulation of the tests using Markov-chain MonteCarlo methods (MCMC) and approximations thereof. See: A. Mohammad-Djafari, “A full bayesian approach for inverse problems,” in Maximum entropy and Bayesian methods. Springer, 1996, pp. 135–144