Tutorials
Wavelets Demystified
| M. Unser |
| Invited presentation, Technical University of Eindhoven, The Netherlands, May 31, 2006. |
|
Abstract:
This 2-hour tutorial focuses on wavelet bases : it covers the concept of multi-resolution analysis, the construction of wavelets,
filterbank algorithms, as well as an in-depth discussion of fundamental wavelet properties.
The presentation is progressive starting with the example of the Haar transform and essentially self contained.
We emphasize the crucial role of splines in wavelet theory, presenting a non-standard point of view
that simplifies the mathematical formulation. The key point is that any wavelet (or scaling function) can
be expressed as the convolution of a (fractional) B-spline and a singular distribution, and that all fundamental spline properties
(reproduction of polynomials, regularity, order of approximation, etc.) are preserved through the convolution operation.
A direct implication is that the wavelets have vanishing moments and that they behave like multiscale differentiators.
These latter two properties are the key for understanding why wavelets yield sparse representations of piecewise-smooth signals.
Bibliography
- M. Unser, M. Unser, "Wavelet Games," Wavelet Digest, vol. 11, no. 4, April 1, 2003.
- S.G. Mallat, "A theory of multiresolution signal decomposition: the wavelet representation," IEEE Trans. Pattern Anal. Machine Intell., vol. PAMI-11, no. 7, pp. 674-693, 1989.
- M. Unser, T. Blu, "Wavelets Theory Demystified," IEEE Trans. Signal Processing, vol. 51, no. 2, pp. 470-483, 2003.
- M. Unser, T. Blu, "Fractional Splines and Wavelets," SIAM Review, vol. 42, no. 1, pp. 43-67, 2000.
- M. Unser, A. Aldroubi, "A Review of Wavelets in Biomedical Applications," Proc. IEEE, vol. 84, no. 4, pp. 626-638, 1996.
|
| M. Unser |
| 2006 IEEE International Symposium on Biomedical Imaging, April 6-9, 2006, Arlington, Virginia, USA. |
|
|
| M. Unser |
| IEEE Signal Processing Magazine, vol. 16, no. 6, pp. 22-38, November 1999. |
| IEEE Signal Processing Society's 2000 Magazine Award |
The goals of this article are three-fold:
- To provide a tutorial on splines that is geared to a signal processing audience.
- To gather all their important properties, and to provide an overview of the mathematical and computational tools available; i.e., a road map for the practitioner with references to the appropriate literature.
- To review the primary applications of splines in signal and image processing.
|
Plenary Talks
| M. Unser |
| 2005 IEEE International Conference on Image Processing (ICIP'05), Genova, Italy, September 11-14, 2005. |
| Slides of the presentation (PDF 9.6 Mb) |
| M. Unser |
| Twentieth GRETSI Symposium on Signal and Image Processing (GRETSI'05), Louvain-la-Neuve, Belgium, September 6-9, 2005. |
| Slides of the presentation (PDF 6.4 Mb) |
| M. Unser |
| 5th International Conference on Scale Space and PDE Methods in Computer Vision, Hofgeismar, Germany, April 6-10, 2005. |
| Slides of the presentation (PDF 10 Mb) |
| M. Unser |
| International Conference on Signal Processing and Communications (SPCOM'04), Bangalore, India, December 11-14, 2004. |
| Slides of the presentation (PDF 5.6 Mb) |
|
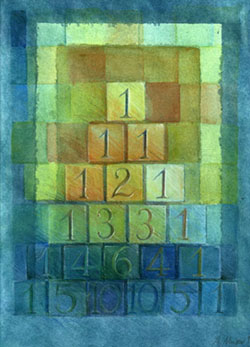
Pascal's triangle: the key for understanding the
connection between splines and wavelet theory.
© 1999 Annette Unser
|