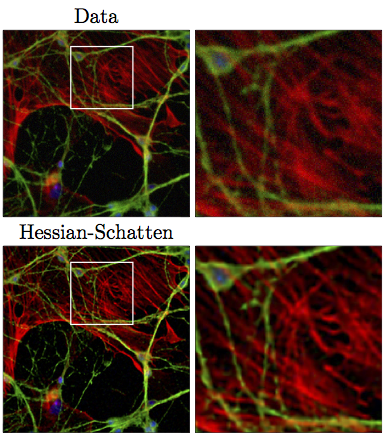
To reconstruct an image from given measurements, one usually solves a so-called inverse problem. The task is carried out by minimizing a cost function that consists of two terms: The first one is a data-fidelity term that ensures consistency with the measurements. The second one is a regularization term that imposes some prior knowledge about the image.
In [1], Lefkimmiatis et al. proposed the Hessian-Schatten seminorm (HS) as a novel regularizer for image reconstruction. Since it is not differentiable, proximal algorithms are the common way to solve the inverse problem. However, there are cases for which proximal algorithms are not applicable (e.g., deep image prior [2] combined with the HS).
In this project, the student will design differentiable approximations of the HS regularizer and implement them within the GlobalBioIm library (Matlab) [3]. The student will then apply the new regularizers on some common inverse problems (e.g., image deconvolution).

References
[1] S. Lefkimmiatis, J. P. Ward and M. Unser, "Hessian Schatten-Norm Regularization for Linear Inverse Problems," in IEEE Transactions on Image Processing, vol. 22, no. 5, pp. 1873-1888, May 2013, doi: 10.1109/TIP.2013.2237919.
[2] Ulyanov, D., Vedaldi, A., & Lempitsky, V. (2018). Deep image prior. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (pp. 9446-9454)
[3] Soubies, E., Soulez, F., McCann, M. T., Pham, T. A., Donati, L., Debarre, T., ... & Unser, M. (2019). Pocket guide to solve inverse problems with GlobalBioIm. Inverse Problems, 35(10), 104006.