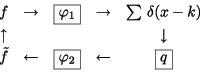
Contrairement à la théorie d'échantillonnage de Shannon, la théorie de l'échantillonnage généralisé postule un modèle selon lequel le signal analogique est d'abord soumis à un filtre de garde non-nécessairement idéal. Ce filtre de garde combine les caractéristiques d'un capteur ou d'un système de mesure. L'échantillonnage proprement dit est ensuite appliqué au signal analogique filtré, et les échantillons produits sont corrigés par un filtre numérique. Enfin, le signal de sortie est analogique; il est construit comme une somme pondérée de translations entières d'une fonction de base prédéfinie. Le filtre de garde et la fonction de base de sortie étant donnés au préalable, la théorie développée à ce jour permet de déterminer un filtre numérique de correction tel que le signal de sortie soit une projection du signal d'entrée. En d'autres termes, si le signal de sortie est réinjecté à l'entrée, alors la nouvelle sortie sera identique à la première. Cette théorie est actuellement unidimensionnelle, scalaire, et synchrone; le premier but du projet est de l'étendre à deux dimensions au moins, et de l'appliquer à des signaux vectoriels. La théorie étendue servira à optimiser l'affichage sur écran à cristeaux liquides d'une image acquise par caméra intégrant un motif de Bayer pour la séparation des couleurs.

Il s'agira ensuite d'étendre la théorie scalaire bidimensionnelle à un cas non-synchrone, dans le sens qu'une opération de suréchantillonnage par deux sera insérée juste après celle d'échantillonnage. La contrainte pour le système d'être une projection sera adaptée en conséquence, en considérant la réinjection d'une réduction analogique par un facteur deux du signal de sortie. Comme dans ce cas la solution est sous-contrainte, on introduira un terme de régularisation pour garantir l'unicité de la solution.