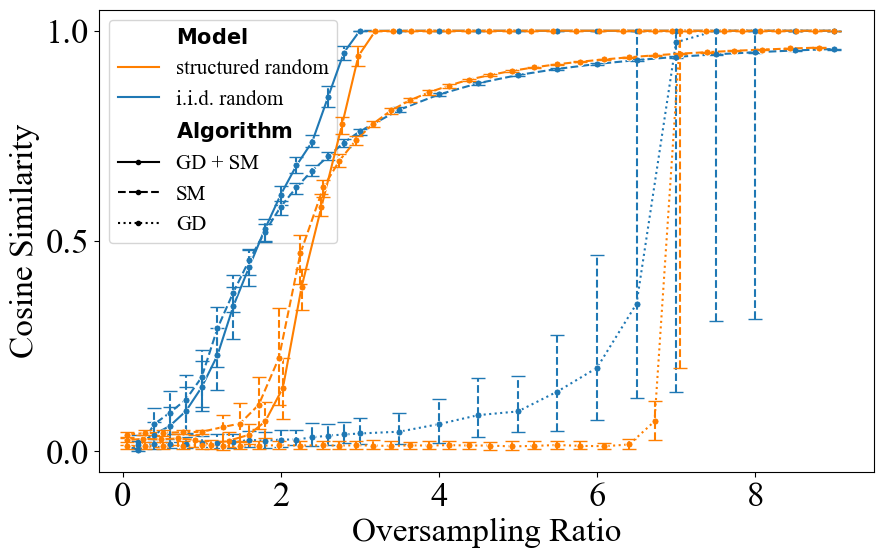
Phase retrieval is the problem of estimating a complex-valued vector given the elementwise modulus of its linear measurements. Structured random models have been proposed to achieve the same performance as i.i.d. random models with substantially faster processing speed. For these models, optimization-based algorithms have been widely used during reconstruction. While a vanilla gradient descent algorithm with proper initialization offers good reconstruction accuracy for structured random models, it usually requires a considerable amount of time to converge, especially near the optimum. Furthermore, it is usually cumbersome to manually finetune the optimal step size for gradient-based algorithms. To overcome these issues, we turn to alternative optimization methods other than the steepest gradient descent to bring acceleration and automation during reconstruction. While there are multiple algorithms offering fast convergence theoretically, it remains unclear which one is the best fit for phase retrieval. This project aims to set the ground for investigation of different optimization methods for phase retrieval through numerical experiments. The student will be provided with a code base containing phase retrieval implementations. Various acceleration strategies such as quasi-Newton and conjugate gradient methods will be implemented explicitly or using automatic differentiation. Besides, it is also possible to investigate acceleration schedules with GPU and automatic parameter selection mechanisms such as linear search. Basic knowledge of Python and optimization is required and experience in PyTorch is recommended.