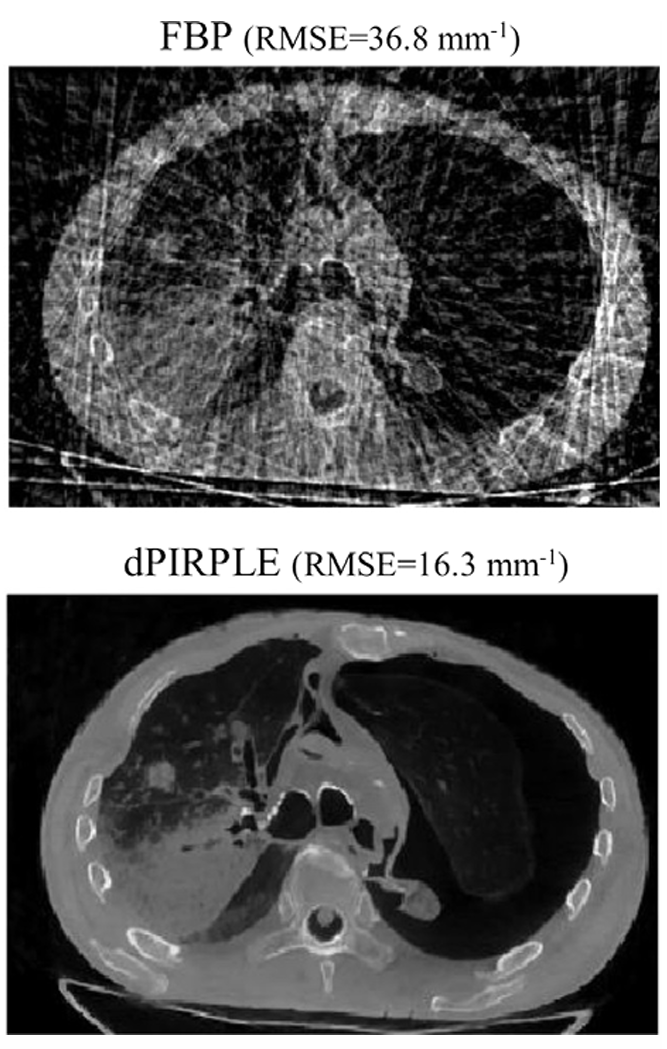
Tomography is widely used in biomedical techniques such as X-ray scans or microscopy. This technique consists in acquiring projection data of an unknown image through the Radon operator. The process of recovering this image is called an Inverse Problem (IP). On one hand the data is most of time corrupted with noise, which may come from the experimental setup, or from the complicated nature of this acquisition process. On the other hand, physical limitations such as limited acquisition angles lead to a lack of data, equivalently, a sub-determined system. Consequently classical techniques fail to recover the original image (cf top image). Modern treatments of this resolution involve the minimization of a loss functional, composed of two terms. A data-fidelity term, which forces the reconstruction to be consistent with the measurements. A regularization term, that promotes a prior belief on the geometrical properties of the image. The choice of regularization is critical as it determines the quality of the reconstruction (cf bottom image), as well as the numerical efficiency of the underlying algorithm. Recently, a new type of regularization was suggested in the form of the tensor-product of two differential operators. This structure should yield a well understood, simple yet qualitative solution to the IP. The student will first be expected to understand the measurement process in tomography and will be provided with build-in numerical simulations of tomography. Then, the student will have to do the numerical implementation of this new regularization along with the building, and the testing, of the optimization pipeline. The project will be carried out in python.