Context
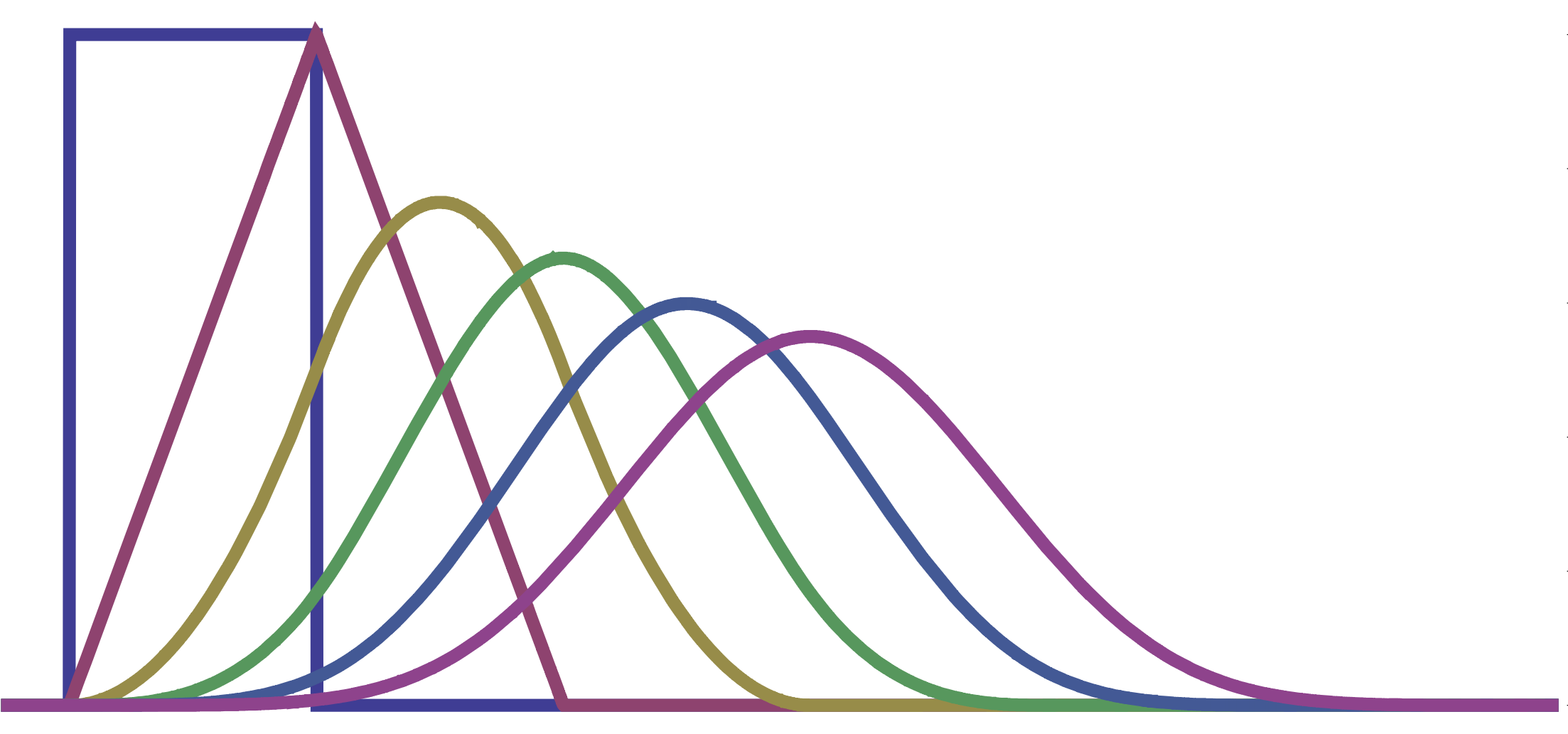
Non-uniform sampling arises in many areas, such as medical imaging, where one obtains noisy, non-uniform samples of a continuous signal f(t). Recovering f(t) from these measurements is an inverse problem, often solved via optimization with a data-fidelity and a regularization term. When the regularizer is the sparsity-promoting L1 norm of L{f}, where L is a differential operator, the solution is known to be an L-spline [1]. Such regularizers are referred to as “generalized total-variation” (gTV). This allows a re-parameterisation of the problem and enables a discrete implementation. This result also holds in a setting more general than that of non-uniform sampling.

Project Outcome
The goal of the project is to recover a continuous-time signal from its noisy non-uniform samples by solving an inverse problem with gTV regularization. The student must first study the theory behind the main result of [1] enabling this project, as well as study the theory of exponential splines and their properties [2]. In particular, B-splines [2] are of interest, due to their desirable properties which the student will be familiar with. The student must then discretize the inverse problem using B-splines and formulate a finite-dimensional optimisation problem. Different optimisation algorithms will then be studied and used to solve this problem. Depending on the student’s advancement, a convergence analysis of the finite-dimensional solution to the true solution can be carried.

Requirements
Good understanding of signal processing and Fourier analysis, with programming skills. Some familiarity with optimization is helpful (key concepts can be learned during the project).

[1] M. Unser, J. Fageot, and J.P. Ward. Splines are universal solutions of linear inverse problems with generalized TV regularization. SIAM Review, 59(4):769–793, 2017.
[2] M. Unser and T. Blu. Cardinal exponential splines: part I - theory and filtering algorithms. IEEE Transactions on Signal Processing, 53(4):1425–1438, 2005.