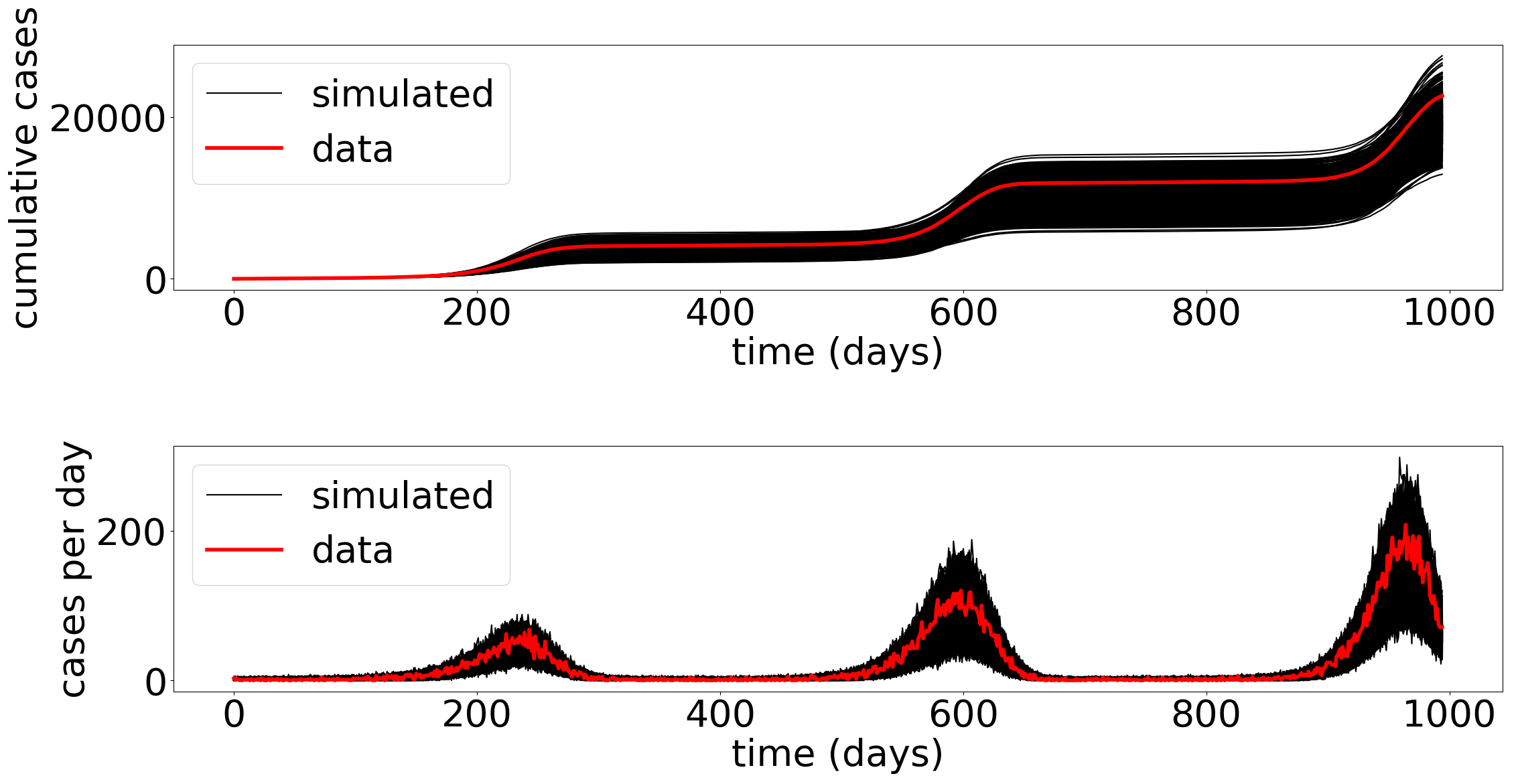
Hawkes processes constitute a family of sparse stochastic point processes used to model self-exciting stochastic phenomenon that arise in epidemiology, belief propagation, biological neural networks, and finance. Their dynamics are governed by an excitation kernel, which, in practice, must be estimated from observed event arrivals. This estimation problem is typically addressed by the maximization of a likelihood function. However, the classical likelihood formulation yields an objective whose number of terms grows with the number of observed events, making optimization computationally demanding, particularly when the process operates near or within a super-critical regime. In this project, the student will investigate a recently proposed binned likelihood designed to mitigate these limitations. The tasks will include the implementation of a routine to simulate Hawkes process trajectories, the programmation of two estimation algorithms: one based on the classical likelihood and one based on the binned likelihood, and a comparative study to evaluate their respective strengths and weaknesses. Proficiency in at least one programming language and a solid understanding of probability theory are recommended.