Talks, Tutorials, and Reviews

Regularization addresses the ill-posedness of the training problem in machine learning or the reconstruction of a signal from a limited number of measurements. The standard strategy consists in augmenting the original cost functional by an energy that penalizes solutions with undesirable behaviour. In this presentation, I will present a general representer theorem that characterizes the solutions of a remarkably broad class of optimization problems in Banach spaces and helps us understand the effect of regularization. I will then use the theorem to retrieve some classical characterizations such as the celebrated representer theorem of machine leaning for RKHS, Tikhonov regularization, representer theorems for sparsity promoting functionals, as well as a few new ones, including a result for deep neural networks.

Regularization is a classical technique for dealing with ill-posed inverse problems; it has been used successfully for biomedical image reconstruction and machine learning.

In this talk, we present a unifying continuous-domain formulation that addresses the problem of recovering a function f from a finite number of linear functionals corrupted by measurement noise. We show that depending on the type of regularization---Tikhonov vs. generalized total variation (gTV)---we obtain very different types of solutions/representer theorems. While the solutions can be interpreted as splines in both cases, the main distinction is that the spline knots are fixed and as many as there are data points in the former setting (classical theory of RKHS), while they are adaptive and few in the case of gTV.

Finally, we consider the problem of the joint optimization of the weights and activation functions in a deep neural network subject to a second-order total variation penalty. The remarkable outcome is that the optimal configuration is achieved with a deep-spline network that can be realized using standard ReLU units. The latter result is compatible with the state-of-the-art in deep learning, but it also suggests some new computational/ optimization challenges.

References

1. M. Unser, J. Fageot, J.P. Ward, "Splines Are Universal Solutions of Linear Inverse Problems with Generalized TV Regularization," SIAM Review, vol. 59, no. 4, pp. 769-793, December 2017.

2. M. Unser, "A Representer Theorem for Deep Neural Networks," arXiv:1802.09210 [stat.ML]

Abstract: Ill-posed inverse problems are often constrained by imposing a bound on the total variation of the solution. Here, we consider a generalized version of total-variation regularization that is tied to some differential operator L. We then show that the general form of the solution is a nonuniform L-spline with fewer knots than the number of measurements. For instance, when L is the derivative operator, then the solution is piecewise constant. The powerful aspect of this characterization is that it applies to any linear inverse problem.

Bio: Michael Unser is currently a Professor and the Director of the Biomedical Imaging Group, EPFL, Lausanne, Switzerland. His primary area of investigation is biomedical image processing. He is internationally recognized for his research contributions to sampling theory, wavelets, the use of splines for image processing, stochastic processes, and computational bioimaging. He has authored over 250 journal papers on those topics.

Sparsity and compressed sensing are very popular topics in signal processing. More and more researchers are relying on l1-type minimization scheme for solving a variety of ill-posed problems in imaging. The paradigm is well established with a solid mathematical foundation, although the arguments that have been put forth in the past are deterministic and finite-dimensional for the most part.

In this presentation, we shall promote a continuous-domain formulation of the problem ("think analog") that is more closely tied to the physics of imaging and that also lends it itself better to mathematical analysis. For instance, we shall demonstrate that splines (which are inherently sparse) are global optimizers of linear inverse problems with total-variation (TV) regularization constraints.

Alternatively, one can adopt an infinite-dimensional statistical point of view by modeling signals as sparse stochastic processes. The guiding principle it then to discretize the inverse problem by projecting both the statistical and physical measurement models onto a linear reconstruction space. This leads to the specification of a general class of maximum a posteriori (MAP) signal estimators complemented with a practical iterative reconstruction scheme ("act digital"). While the framework is compatible with the traditional methods of Tikhonov and TV, it opens the door to a much broader class of potential functions that are inherently sparse, while it also suggests alternative Bayesian recovery procedures. We shall illustrate the approach with the reconstruction of images in a variety of modalities including MRI, phase-contrast tomography, cryo-electron tomography, and deconvolution microscopy. In recent years, significant progress has been achieved in the resolution of ill-posed linear inverse problems by imposing l1/TV regularization constraints on the solution. Such sparsity-promoting schemes are supported by the theory of compressed sensing, which is finite dimensional for the most part.

In recent years, significant progress has been achieved in the resolution of ill-posed linear inverse problems by imposing l1/TV regularization constraints on the solution. Such sparsity-promoting schemes are supported by the theory of compressed sensing, which is finite dimensional for the most part.

In this talk, we take an infinite-dimensional point of view by considering signals that are defined in the continuous domain. We claim that non-uniform splines whose type is matched to the regularization operator are optimal candidate solutions. We show that such functions are global minimizers of a broad family of convex variational problems where the measurements are linear and the regularization is a generalized form of total variation associated with some operator L. We then discuss the link with sparse stochastic processes that are solutions of the same type of differential equations.The pleasing outcome is that the statistical formulation yields maximum a posteriori (MAP) signal estimators that involve the same type of sparsity-promoting regularization, albeit in a discretized form. The latter corresponds to the log-likelihood of the projection of the stochastic model onto a finite-dimensional reconstruction space.

Sparsity is a powerful paradigm for introducing prior constraints on signals in order to address ill-posed image reconstruction problems.

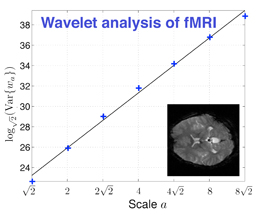
In this talk, we first present a continuous-domain statistical framework that supports the paradigm. We consider stochastic processes that are solutions of non-Gaussian stochastic differential equations driven by white Lévy noise. We show that this yields intrinsically sparse signals in the sense that they admit a concise representation in a matched wavelet basis.

We apply our formalism to the discretization of ill-conditioned linear inverse problems where both the statistical and physical measurement models are projected onto a linear reconstruction space. This leads to the specification of a general class of maximum a posteriori (MAP) signal estimators complemented with a practical iterative reconstruction scheme. While our family of estimators includes the traditional methods of Tikhonov and total-variation (TV) regularization as particular cases, it opens the door to a much broader class of potential functions that are inherently sparse and typically nonconvex. We apply our framework to the reconstruction of images in a variety of modalities including MRI, phase-contrast tomography, cryo-electron tomography, and deconvolution microscopy.

Finally, we investigate the possibility of specifying signal estimators that are optimal in the MSE sense. There, we consider the simpler denoising problem and present a direct solution for first-order processes based on message passing that serves as our goldstandard. We also point out some of the pittfalls of the MAP paradigm (in the non-Gaussian setting) and indicate future directions of research.

We introduce an extended family of continuous-domain sparse processes that are specified by a generic (non-Gaussian) innovation model or, equivalently, as solutions of linear stochastic differential equations driven by white Lévy noise. We present the functional tools for their characterization. We show that their transform-domain probability distributions are infinitely divisible, which induces two distinct types of behavior‐Gaussian vs. sparse‐at the exclusion of any other. This is the key to proving that the non-Gaussian members of the family admit a sparse representation in a matched wavelet basis.

Next, we apply our continuous-domain characterization of the signal to the discretization of ill-conditioned linear inverse problems where both the statistical and physical measurement models are projected onto a linear reconstruction space. This leads the derivation of a general class of maximum a posteriori (MAP) signal estimators. While the formulation is compatible with the standard methods of Tikhonov and l1-type regularizations, which both appear as particular cases, it open the door to a much broader class of sparsity-promoting regularization schemes that are typically nonconvex. We illustrate the concept with the derivation of algorithms for the reconstruction of biomedical images (deconvolution microscopy, MRI, X-ray tomography) from noisy and/or incomplete data. The proposed framework also suggests alternative Bayesian recovery procedures that minimize t he estimation error.

Reference

• M. Unser and P.D. Tafti. An Introduction to Sparse Stochastic Processes, Cambridge University Press, to be published in 2014.
• E. Bostan, U.S. Kamilov, M. Nilchian, M. Unser, "Sparse Stochastic Processes and Discretization of Linear Inverse Problems," IEEE Transactions on Image Processing, vol. 22, no. 7, pp. 2699-2710, July 2013.

We introduce an extended family of sparse processes that are specified by a generic (non-Gaussian) innovation model or, equivalently, as solutions of linear stochastic differential equations driven by white Lévy noise. We present the mathematical tools for their characterization. The two leading threads of the exposition are

• the statistical property of infinite divisibility, which induces two distinct types of behavior-Gaussian vs. sparse-at the exclusion of any other;
• the structural link between linear stochastic processes and splines.

This allows us to prove that these processes admit a parsimonious representation in some matched wavelet-like basis. We show that these models have predictive power for image compression and that they are applicable to the derivation of statistical algorithms for solving ill-posed inverse problems, including compressed sensing.

Our purpose in this talk is to advocate the use of wavelets for advanced biomedical imaging. We start with a short tutorial on wavelet bases, emphasizing the fact that they provide a sparse representation of images. We then discuss a simple, but remarkably effective, image-denoising procedure that essentially amounts to discarding small wavelet coefficients (soft-thresholding). The crucial observation is that this type of “sparsity-promoting” algorithm is the solution of a l1-norm minimization problem. The underlying principle of wavelet regularization is a powerful concept that has been used advantageously for compressed sensing and for reconstructing images from limited and/or noisy measurements. We illustrate the point by presenting wavelet-based algorithms for 3D deconvolution microscopy, and MRI reconstruction (with multiple coils and/or non-Cartesian k-space sampling). These methods were developed at the EPFL in collaboration with imaging scientists and are, for the most part, providing state-of-the-art performance.

The current formulations of compressed sensing and sparse signal recovery are based on solid variational principles, but they are fundamentally deterministic. By drawing on the analogy with the classical theory of signal processing, it is likely that further progress may be achieved by adopting a statistical (or estimation theoretic) point of view. Here, we shall argue that Paul Lévy (1886- 1971), who was one of the very early proponents of Haar wavelets, was in advance over his time, once more. He is the originator of the Lévy-Khinchine formula, which happens to be the perfect (non-Gaussian) ingredient to support a continuous-domain theory of sparse stochastic processes.

Specifically, we shall present an extended class of signal models that are ruled by stochastic differential equations (SDEs) driven by white Léevy noise. Léevy noise is a highly singular mathematical entity that can be interpreted as the weak derivative of a Lévy process. A special case is Gaussian white noise which is the weak derivative of the Wiener process (a.k.a. Brownian motion). When the excitation (or innovation) is Gaussian, the proposed model is equivalent to the traditional one. Of special interest is the property that the signals generated by non-Gaussian linear SDEs tend to be sparse by construction; they also admit a concise representation in some adapted wavelet basis. Moreover, these processes can be (approximately) decoupled by applying a discrete version of the whitening operator (e.g., a finite-difference operator). The corresponding log-likelihood functions, which are nonquadratic, can be specified analytically. In particular, this allows us to uncover a Lévy processes that results in a maximum a posteriori (MAP) estimator that is equivalent to total variation. We make the connection with current methods for the recovery of sparse signals and present some examples of MAP reconstruction of MR images with sparse priors.

We introduce an extended family of continuous-domain stochastic models for sparse, piecewise-smooth signals. These are specified as solutions of stochastic differential equations, or, equivalently, in terms of a suitable innovation model; this is analogous conceptually to the classical interpretation of a Gaussian stationary process as filtered white noise. The non-standard aspect is that the models are driven by non-Gaussian noise (impulsive Poisson or alpha-stable) and that the class of admissible whitening operators is considerably larger than what is allowed in the conventional theory of stationary processes. We provide a complete distributional characterization of these processes. We also introduce signals that are the non-Gaussian (sparse) counterpart of fractional Brownian motion; they are non-stationary and have the same ω-type spectral signature. We prove that our generalized processes have a sparse representation in a wavelet-like basis subject to some mild matching condition. Finally, we discuss implications for sampling and sparse signal recovery.

Wavelets have the remarkable property of providing sparse representations of a wide variety of "natural" images. They have been applied successfully to biomedical image analysis and processing since the early 1990s.

In the first part of this talk, we explain how one can exploit the sparsifying property of wavelets to design more effective algorithms for image denoising and reconstruction, both in terms of quality and computational performance. This is achieved within a variational framework by imposing some ℓ₁-type regularization in the wavelet domain, which favors sparse solutions. We discuss some corresponding iterative skrinkage-thresholding algorithms (ISTA) for sparse signal recovery and introduce a multi-level variant for greater computational efficiency. We illustrate the method with two concrete imaging examples: the deconvolution of 3-D fluorescence micrographs, and the reconstruction of magnetic resonance images from arbitrary (non-uniform) k-space trajectories.

In the second part, we show how to design new wavelet bases that are better matched to the directional characteristics of images. We introduce a general operator-based framework for the construction of steerable wavelets in any number of dimensions. This approach gives access to a broad class of steerable wavelets that are self-reversible and linearly parameterized by a matrix of shaping coefficients; it extends upon Simoncelli's steerable pyramid by providing much greater wavelet diversity. The basic version of the transform (higher-order Riesz wavelets) extracts the partial derivatives of order N of the signal (e.g., gradient or Hessian). We also introduce a signal-adapted design, which yields a PCA-like tight wavelet frame. We illustrate the capabilities of these new steerable wavelets for image analysis and processing (denoising).

The purpose of this talk is to present a modern, unifying perspective of sampling, while demonstrating that the research in this area is still alive and well. We concentrate on the traditional setup where the samples are taken on a uniform grid, but we explicitly take into account the non-ideal nature of the acquisition device and the fact that the measurements may be corrupted by noise. We argue in favor of a variational formulation where the optimal signal reconstruction is specified via a functional optimization problem. The cost to minimize is the sum of a discrete data term and a regularization functional that penalizes non-desirable solutions. We show that, when the regularization is quadratic, the optimal signal reconstruction (among all possible functions) is a generalized spline whose type is tied to the regularization operator. This leads to an optimal discretization and an efficient signal reconstruction in terms of generalized B-spline basis functions. A possible variation is to penalize the L1-norm of the derivative of the function (total variation), which can also be achieved within the spline framework via a suitable knot deletion process.
The theory of compressed sensing provides an alternative approach to sampling that is qualitatively similar to total-variation regularization. Here the idea to favor solutions that have a sparse representation in a wavelet basis. Practically, this is achieved by imposing a regularization constraint on the l1-norm of the wavelet coefficients. We show that the corresponding inverse problem can be solved efficiently via a multi-scale variant of the ISTA algorithm (iterative skrinkage-thresholding). We illustrate the method with two concrete imaging examples: the deconvolution of 3-D fluorescence micrographs, and the reconstruction of magnetic resonance images from arbitrary (non-uniform) k-space trajectories.

This tutorial will explain the modern, Hilbert-space approach for the discretization (sampling) and reconstruction (interpolation) of images (in two or higher dimensions). The emphasis will be on quality and optimality, which are important considerations for biomedical applications.
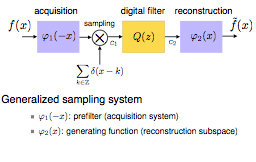
The main point in the modern formulation is that the signal model need not be bandlimited. In fact, it makes much better sense computationally to consider spline or wavelet-like representations that involve much shorter (e.g. compactly supported) basis functions that are shifted replicates of a single prototype (e.g., B-spline). We will show how Shannon's standard sampling paradigm can be adapted for dealing with such representations. In essence, this boils down to modifying the classical "anti-aliasing" prefilter so that it is optimally matched to the representation space (in practice, this can be accomplished by suitable digital post-filtering). We will also discuss efficient digital-filter-based solutions for high-quality image interpolation. Another important issue will be the assessment of interpolation quality and the identification of basis functions (and interpolators) that offer the best performance for a given computational budget. These concepts will be illustrated with various applications in biomedical imaging: tomographic reconstruction, 3D slicing and re-formatting, estimation of image differentials for feature extraction, and image registration (both rigid-body and elastic).

This tutorial will explain the modern, Hilbert-space approach for the discretization (sampling) and reconstruction (interpolation) of images (in two or higher dimensions). The emphasis will be on quality and optimality, which are important considerations for biomedical applications.

The main point in the modern formulation is that the signal model need not be bandlimited. In fact, it makes much better sense computationally to consider spline or wavelet-like representations that involve much shorter (e.g. compactly supported) basis functions that are shifted replicates of a single prototype (e.g., B-spline). We will show how Shannon's standard sampling paradigm can be adapted for dealing with such representations. In essence, this boils down to modifying the classical "anti-aliasing" prefilter so that it is optimally matched to the representation space (in practice, this can be accomplished by suitable digital post-filtering). Another important issue will be the assessment of interpolation quality and the identification of basis functions (and interpolators) that offer the best performance for a given computational budget.

Reference: M. Unser, "Sampling—50 Years After Shannon," Proceedings of the IEEE, vol. 88, no. 4, pp. 569-587, April 2000.

We start our account of inverse problems in imaging with a brief review of first-generation reconstruction algorithms, which are linear and typically non-iterative (e.g., backprojection). We then highlight the emergence of the concept of sparsity, which opened the door to the resolution of more difficult image reconstruction problems, including compressed sensing. In particular, we demonstrate the global optimality of splines for solving problems with total-variation (TV) regularization constraints. Next, we introduce an alternative statistical formulation where signals are modeled as sparse stochastic processes. This allows us to establish a formal equivalence between non-Gaussian MAP estimation and sparsity-promoting techniques that are based on the minimization of a non-quadratic cost functional. We also show how to compute the solution efficiently via an alternating sequence of linear steps and pointwise nonlinearities (ADMM algorithm). This concludes our discussion of the second-generation methods that constitute the state-of-the-art in a variety of modalities.

In the final part of the presentation, we shall argue that learning techniques will play a central role in the future development of the field with the emergence of third-generation methods. A natural solution for improving image quality is to retain the linear part of the ADMM algorithm while optimizing its non-linear step (proximal operator) so as to minimize the reconstruction error. Another more extreme scenario is to replace the iterative part of the reconstruction by a deep convolutional network. The various approaches will be illustrated with the reconstruction of images in a variety of modalities including MRI, X-ray and cryo-electron tomography, and deconvolution microscopy.

A fundamental component of the imaging pipeline is the reconstruction algorithm. In this educational session, we review the physical and mathematical principles that underlie the design of such algorithms. We argue that the concepts are fairly universal and applicable to a majority of (bio)medical imaging modalities, including magnetic resonance imaging and fMRI, x-ray computer tomography, and positron-emission tomography (PET). Interestingly, the paradigm remains valid for modern cellular/molecular imaging with confocal/super-resolution fluorescence microscopy, which is highly relevant to molecular imaging as well. In fact, we believe that the huge potential for cross-fertilization and mutual re-enforcement between imaging modalities has not been fully exploited yet.

The prerequisite to image reconstruction is an accurate physical description of the image-formation process: the so-called forward model, which is assumed to be linear. Numerically, this translates into the specification of a system matrix, while the reconstruction of images conceptually boils down to a stable inversion of this matrix. The difficulty is essentially twofold: (i) the system matrix is usually much too large to be stored/inverted directly, and (ii) the problem is inherently ill-posed due to the presence of noise and/or bad conditioning of the system.

Our starting point is an overview of the modalities in relation to their forward model. We then discuss the classical linear reconstruction methods that typically involve some form of backpropagation (CT or PET) and/or the fast Fourier transform (in the case of MRI). We present stabilized variants of these methods that rely on (Tikhonov) regularization or the injection of prior statistical knowledge under the Gaussian hypothesis. Next, we review modern iterative schemes that can handle challenging acquisition setups such as parallel MRI, non-Cartesian sampling grids, and/or missing views. In particular, we discuss sparsity-promoting methods that are supported by the theory of compressed sensing. We show how to implement such schemes efficiently using simple combinations of linear solvers and thresholding operations. The main advantage of these recent algorithms is that they improve the quality of the image reconstruction. Alternatively, they allow a substantial reduction of the radiation dose and/or acquisition time without noticeable degradation in quality. This behavior is illustrated practically.

In the final part of the tutorial, we discuss the current challenges and directions of research in the field; in particular, the necessity of dealing with large data sets in multiple dimensions: 2D or 3D space combined with time (in the case of dynamic imaging) and/or multispectral/multimodal information.

While the major achievements in medical imaging can be traced back to the end the 20th century, there are strong indicators that we have recently entered the golden age of cellular/biological imaging. The enabling modality is fluorescence microscopy which results from the combination of highly specific fluorescent probes (Nobel Prize 2008) and sophisticated optical instrumentation (Nobel Prize 2014). This has led to the emergence of modern microscopy centers that are providing biologists with unprecedented amounts of data in 3D + time.

To address the computational aspects, two nascent fields have emerged in which image processing is expected to play a significant role. The first is "digital optics" where the idea is to combine optics with advanced signal processing in order to increase spatial resolution while reducing acquisition time. The second area is "bioimage informatics" which is concerned with the development of image analysis software to make microscopy more quantitative. The key issue here is reliable image segmentation as well as the ability to track structures of interest over time. We shall discuss specific examples and describe state-of-the-art solutions for bioimage reconstruction and analysis. This will help us build a list of challenges and opportunities to guide further research in bioimaging.

We introduce an extended family of continuous-domain sparse processes that are specified by a generic (non-Gaussian) innovation model or, equivalently, as solutions of linear stochastic differential equations driven by white Lévy noise. We present the functional tools for their characterization. We show that their transform-domain probability distributions are infinitely divisible, which induces two distinct types of behavior‐Gaussian vs. sparse‐at the exclusion of any other. This is the key to proving that the non-Gaussian members of the family admit a sparse representation in a matched wavelet basis.

Next, we apply our continuous-domain characterization of the signal to the discretization of ill-conditioned linear inverse problems where both the statistical and physical measurement models are projected onto a linear reconstruction space. This leads the derivation of a general class of maximum a posteriori (MAP) signal estimators. While the formulation is compatible with the standard methods of Tikhonov and l1-type regularizations, which both appear as particular cases, it open the door to a much broader class of sparsity-promoting regularization schemes that are typically nonconvex. We illustrate the concept with the derivation of algorithms for the reconstruction of biomedical images (deconvolution microscopy, MRI, X-ray tomography) from noisy and/or incomplete data. The proposed framework also suggests alternative Bayesian recovery procedures that minimize t he estimation error.

Reference

• M. Unser and P.D. Tafti. An Introduction to Sparse Stochastic Processes, Cambridge University Press, to be published in 2014.
• E. Bostan, U.S. Kamilov, M. Nilchian, M. Unser, "Sparse Stochastic Processes and Discretization of Linear Inverse Problems," IEEE Transactions on Image Processing, vol. 22, no. 7, pp. 2699-2710, July 2013.

Our purpose in this talk is to advocate the use of wavelets for advanced biomedical imaging. We start with a short tutorial on wavelet bases, emphasizing the fact that they provide a sparse representation of images. We then discuss a simple, but remarkably effective, image-denoising procedure that essentially amounts to discarding small wavelet coefficients (soft-thresholding). The crucial observation is that this type of “sparsity-promoting” algorithm is the solution of a l1-norm minimization problem. The underlying principle of wavelet regularization is a powerful concept that has been used advantageously for compressed sensing and for reconstructing images from limited and/or noisy measurements. We illustrate the point by presenting wavelet-based algorithms for 3D deconvolution microscopy, and MRI reconstruction (with multiple coils and/or non-Cartesian k-space sampling). These methods were developed at the EPFL in collaboration with imaging scientists and are, for the most part, providing state-of-the-art performance.

Wavelets have the remarkable property of providing sparse representations of a wide variety of "natural" images. They have been applied successfully to biomedical image analysis and processing since the early 1990s.

In the first part of this talk, we explain how one can exploit the sparsifying property of wavelets to design more effective algorithms for image denoising and reconstruction, both in terms of quality and computational performance. This is achieved within a variational framework by imposing some ℓ₁-type regularization in the wavelet domain, which favors sparse solutions. We discuss some corresponding iterative skrinkage-thresholding algorithms (ISTA) for sparse signal recovery and introduce a multi-level variant for greater computational efficiency. We illustrate the method with two concrete imaging examples: the deconvolution of 3-D fluorescence micrographs, and the reconstruction of magnetic resonance images from arbitrary (non-uniform) k-space trajectories.

In the second part, we show how to design new wavelet bases that are better matched to the directional characteristics of images. We introduce a general operator-based framework for the construction of steerable wavelets in any number of dimensions. This approach gives access to a broad class of steerable wavelets that are self-reversible and linearly parameterized by a matrix of shaping coefficients; it extends upon Simoncelli's steerable pyramid by providing much greater wavelet diversity. The basic version of the transform (higher-order Riesz wavelets) extracts the partial derivatives of order N of the signal (e.g., gradient or Hessian). We also introduce a signal-adapted design, which yields a PCA-like tight wavelet frame. We illustrate the capabilities of these new steerable wavelets for image analysis and processing (denoising).

This tutorial will explain the modern, Hilbert-space approach for the discretization (sampling) and reconstruction (interpolation) of images (in two or higher dimensions). The emphasis will be on quality and optimality, which are important considerations for biomedical applications.
The main point in the modern formulation is that the signal model need not be bandlimited. In fact, it makes much better sense computationally to consider spline or wavelet-like representations that involve much shorter (e.g. compactly supported) basis functions that are shifted replicates of a single prototype (e.g., B-spline). We will show how Shannon's standard sampling paradigm can be adapted for dealing with such representations. In essence, this boils down to modifying the classical "anti-aliasing" prefilter so that it is optimally matched to the representation space (in practice, this can be accomplished by suitable digital post-filtering). We will also discuss efficient digital-filter-based solutions for high-quality image interpolation. Another important issue will be the assessment of interpolation quality and the identification of basis functions (and interpolators) that offer the best performance for a given computational budget. These concepts will be illustrated with various applications in biomedical imaging: tomographic reconstruction, 3D slicing and re-formatting, estimation of image differentials for feature extraction, and image registration (both rigid-body and elastic).

With the recent development of fluorescent probes and new high-resolution microscopes, biological imaging has entered a new era and is presently having a profound impact on the way research is being conducted in the life sciences. Biologists have come to depend more and more on imaging. They can now visualize subcellular components and processes in vivo, both structurally and functionally. Observations can be made in two or three dimensions, at different wavelengths (spectroscopy), possibly with time-lapse imaging to investigate cellular dynamics.

The observation of many biological processes relies on the ability to identify and locate specific proteins within their cellular environment. Cells are mostly transparent in their natural state and the immense number of molecules that constitute them are optically indistinguishable from one another. This makes the identification of a particular protein a very complex task—akin to finding a needle in a haystack.

Sparsity and compressed sensing are very popular topics in signal processing. More and more researchers are relying on l1-type minimization scheme for solving a variety of ill-posed problems in imaging. The paradigm is well established with a solid mathematical foundation, although the arguments that have been put forth in the past are deterministic and finite-dimensional for the most part.

In this presentation, we shall promote a continuous-domain formulation of the problem ("think analog") that is more closely tied to the physics of imaging and that also lends it itself better to mathematical analysis. For instance, we shall demonstrate that splines (which are inherently sparse) are global optimizers of linear inverse problems with total-variation (TV) regularization constraints.

Alternatively, one can adopt an infinite-dimensional statistical point of view by modeling signals as sparse stochastic processes. The guiding principle it then to discretize the inverse problem by projecting both the statistical and physical measurement models onto a linear reconstruction space. This leads to the specification of a general class of maximum a posteriori (MAP) signal estimators complemented with a practical iterative reconstruction scheme ("act digital"). While the framework is compatible with the traditional methods of Tikhonov and TV, it opens the door to a much broader class of potential functions that are inherently sparse, while it also suggests alternative Bayesian recovery procedures. We shall illustrate the approach with the reconstruction of images in a variety of modalities including MRI, phase-contrast tomography, cryo-electron tomography, and deconvolution microscopy. In recent years, significant progress has been achieved in the resolution of ill-posed linear inverse problems by imposing l1/TV regularization constraints on the solution. Such sparsity-promoting schemes are supported by the theory of compressed sensing, which is finite dimensional for the most part.

In recent years, significant progress has been achieved in the resolution of ill-posed linear inverse problems by imposing l1/TV regularization constraints on the solution. Such sparsity-promoting schemes are supported by the theory of compressed sensing, which is finite dimensional for the most part.

In this talk, we take an infinite-dimensional point of view by considering signals that are defined in the continuous domain. We claim that non-uniform splines whose type is matched to the regularization operator are optimal candidate solutions. We show that such functions are global minimizers of a broad family of convex variational problems where the measurements are linear and the regularization is a generalized form of total variation associated with some operator L. We then discuss the link with sparse stochastic processes that are solutions of the same type of differential equations.The pleasing outcome is that the statistical formulation yields maximum a posteriori (MAP) signal estimators that involve the same type of sparsity-promoting regularization, albeit in a discretized form. The latter corresponds to the log-likelihood of the projection of the stochastic model onto a finite-dimensional reconstruction space.

Plenary talk, Seventh Biennial Conference, 2004 International Conference on Signal Processing and Communications (SPCOM'04), Bangalore, India, December 11-14, 2004.

By interpreting the Green-function reproduction property of exponential splines in signal-processing terms, we uncover a fundamental relation that connects the impulse responses of all-pole analog filters to their discrete counterparts. The link is that the latter are the B-spline coefficients of the former (which happen to be exponential splines). Motivated by this observation, we introduce an extended family of cardinal splines—the generalized E-splines—to generalize the concept for all convolution operators with rational transfer functions. We construct the corresponding compactly supported B-spline basis functions which are characterized by their poles and zeros, thereby establishing an interesting connection with analog-filter design techniques. We investigate the properties of these new B-splines and present the corresponding signal-processing calculus, which allows us to perform continuous-time operations such as convolution, differential operators, and modulation, by simple application of the discrete version of these operators in the B-spline domain. In particular, we show how the formalism can be used to obtain exact, discrete implementations of analog filters. We also apply our results to the design of hybrid signal-processing systems that rely on digital filtering to compensate for the non-ideal characteristics of real-world A-to-D and D-to-A conversion systems.

We introduce a Hilbert-space framework, inspired by wavelet theory, that provides an exact link between the traditional—discrete and analog—formulations of signal processing. In contrast to Shannon's sampling theory, our approach uses basis functions that are compactly supported and therefore better suited for numerical computations. The underlying continuous-time signal model is of exponential spline type (with rational transfer function); this family of functions has the advantage of being closed under the basic signal-processing operations: differentiation, continuous-time convolution, and modulation. A key point of the method is that it allows an exact implementation of continuous-time operators by simple processing in the discrete domain, provided that one updates the basis functions appropriately. The framework is ideally suited for hybrid signal processing because it can jointly represent the effect of the various (analog or digital) components of the system. This point will be illustrated with the design of hybrid systems for improved A-to-D and D-to-A conversion. On the more fundamental front, the proposed formulation sheds new light on the striking parallel that exists between the basic analog and discrete operators in the classical theory of linear systems.

Our purpose is to justify the use splines in imaging applications, emphasizing their ease of use, as well as their fundamental properties. Modeling images with splines is painless: it essentially amounts to replacing the pixels by B-spline basis functions, which are piecewise polynomials with a maximum order of differentiability. The spline representation is flexible and provides the best cost/quality tradeoff among all interpolation methods: by increasing the degree, one shifts from a simple piecewise linear representation to a higher order one that gets closer and closer to being bandlimited. We will describe efficient digital filter-based algorithms for interpolating and processing images within this framework. We will also discuss the multiresolution properties of splines that make them especially attractive for multi-scale processing.
On the more fundamental front, we will show that splines are intimately linked to differentials; in fact, the B-splines are the exact mathematical translators between the discrete and continuous versions of the operator. This is probably the reason why these functions play such a fundamental role in wavelet theory. Splines may also be justified on variational or statistical grounds; in particular, they can be shown to be optimal for the representation of fractal-like signals.
We will illustrate spline processing with applications in biomedical imaging where its impact has been the greatest so far. Specific tasks include high-quality interpolation, image resizing, tomographic reconstruction and various types of image registration.

We consider the generalized sampling problem with non-ideal acquisition device. The task is to “optimally” reconstruct a continuously-varying input signal from its discrete, noisy measurements in some integer-shift-invariant space. We propose three formulations of the problem—variational/Tikhonov, minimax, and minimum mean square error estimation—and derive the corresponding solutions for a given reconstruction space. We prove that these solutions are also globally-optimal, provided that the reconstruction space is matched to the regularization operator (deterministic signal) or, alternatively, to the whitening operator of the process (stochastic modeling). Moreover, the three formulations lead to the same generalized smoothing spline reconstruction algorithm, but only if the reconstruction space is chosen optimally. We then show that fractional splines and fractal processes (fBm) are solutions of the same type of differential equations, except that the context is different: deterministic versus stochastic. We use this link to provide a solid stochastic justification of spline-based reconstruction algorithms. Finally, we propose a novel formulation of vector-splines based on similar principles, and demonstrate their application to flow field reconstruction from non-uniform, incomplete ultrasound Doppler data.

This is joint work with Yonina Eldar, Thierry Blu, and Muthuvel Arigovindan.

"Think analog, act digital" is a motto that is relevant to scientific computing and algorithm design in a variety of disciplines, including numerical analysis, image/signal processing, and computer graphics.
Here, we will argue that cardinal splines constitute a theoretical and computational framework that is ideally matched to this philosophy, especially when the data is available on a uniform grid.
We show that multidimensional spline interpolation or approximation can be performed most efficiently using recursive digital filtering techniques. We highlight a number of "optimal" aspects of splines (in particular, polynomial ones) and discuss fundamental relations with: (1) Shannon's sampling theory, (2) linear system theory, (3) wavelet theory, (4) regularization theory, (5) estimation theory, and (6) stochastic processes (in particular, fractals). The practicality of the spline framework is illustrated with concrete image processing examples; these include derivative-based feature extraction, high-quality rotation and scaling, and (rigid body or elastic) image registration.

Six talks on the work of the 2017-2020 Abel Prize Laureates.

In recent years, significant progress has been achieved in the resolution of ill-posed linear inverse problems by imposing l1/TV regularization constraints on the solution. Such sparsity-promoting schemes are supported by the theory of compressed sensing, which is finite dimensional for the most part.

In this talk, we take an infinite-dimensional point of view by considering signals that are defined in the continuous domain. We claim that non-uniform splines whose type is matched to the regularization operator are optimal candidate solutions. We show that such functions are global minimizers of a broad family of convex variational problems where the measurements are linear and the regularization is a generalized form of total variation associated with some operator L. We then discuss the link with sparse stochastic processes that are solutions of the same type of differential equations.The pleasing outcome is that the statistical formulation yields maximum a posteriori (MAP) signal estimators that involve the same type of sparsity-promoting regularization, albeit in a discretized form. The latter corresponds to the log-likelihood of the projection of the stochastic model onto a finite-dimensional reconstruction space.

Our purpose in this talk is to advocate the use of wavelets for advanced biomedical imaging. We start with a short tutorial on wavelet bases, emphasizing the fact that they provide a sparse representation of images. We then discuss a simple, but remarkably effective, image-denoising procedure that essentially amounts to discarding small wavelet coefficients (soft-thresholding). The crucial observation is that this type of “sparsity-promoting” algorithm is the solution of a l1-norm minimization problem. The underlying principle of wavelet regularization is a powerful concept that has been used advantageously for compressed sensing and for reconstructing images from limited and/or noisy measurements. We illustrate the point by presenting wavelet-based algorithms for 3D deconvolution microscopy, and MRI reconstruction (with multiple coils and/or non-Cartesian k-space sampling). These methods were developed at the EPFL in collaboration with imaging scientists and are, for the most part, providing state-of-the-art performance.

Wavelets have the remarkable property of providing sparse representations of a wide variety of "natural" images. They have been applied successfully to biomedical image analysis and processing since the early 1990s.

In the first part of this talk, we explain how one can exploit the sparsifying property of wavelets to design more effective algorithms for image denoising and reconstruction, both in terms of quality and computational performance. This is achieved within a variational framework by imposing some ℓ₁-type regularization in the wavelet domain, which favors sparse solutions. We discuss some corresponding iterative skrinkage-thresholding algorithms (ISTA) for sparse signal recovery and introduce a multi-level variant for greater computational efficiency. We illustrate the method with two concrete imaging examples: the deconvolution of 3-D fluorescence micrographs, and the reconstruction of magnetic resonance images from arbitrary (non-uniform) k-space trajectories.

In the second part, we show how to design new wavelet bases that are better matched to the directional characteristics of images. We introduce a general operator-based framework for the construction of steerable wavelets in any number of dimensions. This approach gives access to a broad class of steerable wavelets that are self-reversible and linearly parameterized by a matrix of shaping coefficients; it extends upon Simoncelli's steerable pyramid by providing much greater wavelet diversity. The basic version of the transform (higher-order Riesz wavelets) extracts the partial derivatives of order N of the signal (e.g., gradient or Hessian). We also introduce a signal-adapted design, which yields a PCA-like tight wavelet frame. We illustrate the capabilities of these new steerable wavelets for image analysis and processing (denoising).

We introduce an Nth-order extension of the Riesz transform that has the remarkable property of mapping any primary wavelet frame (or basis) of L2(ℝ²) into another "steerable" wavelet frame, while preserving the frame bounds. Concretely, this means we can design reversible multi-scale decompositions in which the analysis wavelets (feature detectors) can be spatially rotated in any direction via a suitable linear combination of wavelet coefficients. The concept provides a rigorous functional counterpart to Simoncelli's steerable pyramid whose construction was entirely based on digital filter design. It allows for the specification of wavelets with any order of steerability in any number of dimensions. We illustrate the method with the design of new steerable polyharmonic-spline wavelets that replicate the behavior of the Nth-order partial derivatives of an isotropic Gaussian kernel.
The case N=1 is of special interest because it provides a functional framework for performing wavelet-domain monogenic signal analyses. Specifically we introduce a monogenic wavelet representation of images where each wavelet index is associated with a local orientation, an amplitude and a phase. We present examples of applications to directional image analyses and coherent optical imaging.

Invariance is an attractive principle for specifying image processing algorithms. In this presentation, we promote affine invariance—more precisely, invariance with respect to translation, scaling and rotation. As starting point, we identify the corresponding class of invariant 2D operators: these are combinations of the (fractional) Laplacian and the complex gradient (or Wirtinger operator). We then specify some corresponding differential equation and show that the solution in the real-valued case is either a fractional Brownian field or a polyharmonic spline, depending on the nature of the system input (driving term): stochastic (white noise) or deterministic (stream of Dirac impulses). The affine invariance of the operator has two important consequences: (1) the statistical self-similarity of the fractional Brownian field, and (2) the fact that the polyharmonic splines specify a multiresolution analysis of L₂(ℝ²) and lend themselves to the construction of wavelet bases. The other fundamental implication is that the corresponding wavelets behave like multi-scale versions of the operator from which they are derived; this makes them ideally suited for the analysis of multidimensional signals with fractal characteristics (whitening property of the fractional Laplacian) [1].

The complex extension of the approach yields a new complex wavelet basis that replicates the behavior of the Laplace-gradient operator and is therefore adapted to edge detection [2]. We introduce the Marr wavelet pyramid which corresponds to a slightly redundant version of this transform with a Gaussian-like smoothing kernel that has been optimized for better steerability. We demonstrate that this multiresolution representation is well suited for a variety of image-processing tasks. In particular, we use it to derive a primal wavelet sketch—a compact description of the image by a multiscale, subsampled edge map—and provide a corresponding iterative reconstruction algorithm.

References:
[1] P.D. Tafti, D. Van De Ville, M. Unser, "Invariances, Laplacian-Like Wavelet Bases, and the Whitening of Fractal Processes," IEEE Transactions on Image Processing, vol. 18, no. 4, pp. 689-702, April 2009.
[2] D. Van De Ville, M. Unser, "Complex Wavelet Bases, Steerability, and the Marr-Like Pyramid," IEEE Transactions on Image Processing, vol. 17, no. 11, pp. 2063-2080, November 2008.

Invariance is an attractive principle for specifying image processing algorithms. In this work, we concentrate on affine—more precisely, shift, scale and rotation—invariance and identify the corresponding class of operators, which are fractional Laplacians. We then specify some corresponding differential equation and show that the solution (in the distributional sense) is either a fractional Brownian field (Mandelbrot and Van Ness, 1968) or a polyharmonic spline (Duchon, 1976), depending on the nature of the system input (driving term): stochastic (white noise) or deterministic (stream of Dirac impulses). The affine invariance of the operator has two remarkable consequences: (1) the statistical self-similarity of the fractional Brownian field, and (2) the fact that the polyharmonic splines specify a multiresolution analysis of L₂(ℝ^d) and lend themselves to the construction of wavelet bases. We prove that these wavelets essentially behave like the operator from which they are derived, and that they are ideally suited for the analysis of multidimensional signals with fractal characteristics (isotopic differentiation, and whitening property).

This is joint work with Pouya Tafti and Dimitri Van De Ville.

This paper presents an account of the current state of sampling, 50 years after Shannon's formulation of the sampling theorem. The emphasis is on regular sampling where the grid is uniform. This topic has benefited from a strong research revival during the past few years, thanks in part to the mathematical connections that were made with wavelet theory. To introduce the reader to the modern, Hilbert-space formulation, we re-interpret Shannon's sampling procedure as an orthogonal projection onto the subspace of bandlimited functions. We then extend the standard sampling paradigm for a representation of functions in the more general class of "shift-invariant" functions spaces, including splines and wavelets. Practically, this allows for simpler—and possibly more realistic—interpolation models, which can be used in conjunction with a much wider class of (anti-aliasing) pre-filters that are not necessarily ideal lowpass. We summarize and discuss the results available for the determination of the approximation error and of the sampling rate when the input of the system is essentially arbitrary; e.g., non-bandlimited. We also review variations of sampling that can be understood from the same unifying perspective. These include wavelets, multi-wavelets, Papoulis generalized sampling, finite elements, and frames. Irregular sampling and radial basis functions are briefly mentioned.

A fundamental component of the imaging pipeline is the reconstruction algorithm. In this educational session, we review the physical and mathematical principles that underlie the design of such algorithms. We argue that the concepts are fairly universal and applicable to a majority of (bio)medical imaging modalities, including magnetic resonance imaging and fMRI, x-ray computer tomography, and positron-emission tomography (PET). Interestingly, the paradigm remains valid for modern cellular/molecular imaging with confocal/super-resolution fluorescence microscopy, which is highly relevant to molecular imaging as well. In fact, we believe that the huge potential for cross-fertilization and mutual re-enforcement between imaging modalities has not been fully exploited yet.

The prerequisite to image reconstruction is an accurate physical description of the image-formation process: the so-called forward model, which is assumed to be linear. Numerically, this translates into the specification of a system matrix, while the reconstruction of images conceptually boils down to a stable inversion of this matrix. The difficulty is essentially twofold: (i) the system matrix is usually much too large to be stored/inverted directly, and (ii) the problem is inherently ill-posed due to the presence of noise and/or bad conditioning of the system.

Our starting point is an overview of the modalities in relation to their forward model. We then discuss the classical linear reconstruction methods that typically involve some form of backpropagation (CT or PET) and/or the fast Fourier transform (in the case of MRI). We present stabilized variants of these methods that rely on (Tikhonov) regularization or the injection of prior statistical knowledge under the Gaussian hypothesis. Next, we review modern iterative schemes that can handle challenging acquisition setups such as parallel MRI, non-Cartesian sampling grids, and/or missing views. In particular, we discuss sparsity-promoting methods that are supported by the theory of compressed sensing. We show how to implement such schemes efficiently using simple combinations of linear solvers and thresholding operations. The main advantage of these recent algorithms is that they improve the quality of the image reconstruction. Alternatively, they allow a substantial reduction of the radiation dose and/or acquisition time without noticeable degradation in quality. This behavior is illustrated practically.

In the final part of the tutorial, we discuss the current challenges and directions of research in the field; in particular, the necessity of dealing with large data sets in multiple dimensions: 2D or 3D space combined with time (in the case of dynamic imaging) and/or multispectral/multimodal information.

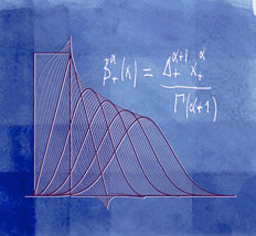
We extend Schoenberg's family of polynomial splines with uniform knots to all fractional degrees α > -1. These splines, which involve linear combinations of the one-sided power functions x₊^α = max(0, x)^α, belong to L¹ and are α-Hölder continuous for α > 0. We construct the corresponding B-splines by taking fractional finite differences and provide an explicit characterization in both time and frequency domains. We show that these functions satisfy most of the properties of the traditional B-splines, including the convolution property, and a generalized fractional differentiation rule that involves finite differences only. We characterize the decay of the B-splines which are not compactly supported for non-integral α's. Their most astonishing feature (in reference to the Strang-Fix theory) is that they have a fractional order of approximation α + 1 while they reproduce the polynomials of degree [α]. For α > 1/2, they satisfy all the requirements for a multiresolution analysis of L² (Riesz bounds, two scale relation) and may therefore be used to build new families of wavelet bases with a continuously-varying order parameter. Our construction also yields symmetrized fractional B-splines which provide the connection with Duchon's general theory of radial (m,s)-splines (including thin-plate splines). In particular, we show that the symmetric version of our splines can be obtained as solution of a variational problem involving the norm of a fractional derivative.

We extend Schoenberg's family of polynomial splines with uniform knots to all fractional degrees α > -1. These splines, which involve linear combinations of the one-sided power functions x₊^α = max(0, x)^α, belong to L¹ and are α-Hölder continuous for α > 0. We construct the corresponding B-splines by taking fractional finite differences and provide an explicit characterization in both time and frequency domains. We show that these functions satisfy most of the properties of the traditional B-splines, including the convolution property, and a generalized fractional differentiation rule that involves finite differences only. We characterize the decay of the B-splines which are not compactly supported for non-integral α's. Their most astonishing feature (in reference to the Strang-Fix theory) is that they have a fractional order of approximation α + 1 while they reproduce the polynomials of degree [α]. For α > 1/2, they satisfy all the requirements for a multiresolution analysis of L² (Riesz bounds, two scale relation) and may therefore be used to build new families of wavelet bases with a continuously-varying order parameter. Our construction also yields symmetrized fractional B-splines which provide the connection with Duchon's general theory of radial (m,s)-splines (including thin-plate splines). In particular, we show that the symmetric version of our splines can be obtained as solution of a variational problem involving the norm of a fractional derivative.

Summary: A dialogue between father and son about wavelets, Legos, and other existential questions.

For the first time, the field's leading international experts have come together to produce a complete guide to wavelet transform applications in medicine and biology. This book provides guidelines for all those interested in learning about waveletes and their applications to biomedical problems.

The introductory material is written for non-experts and includes basic discussions of the theoretical and practical foundations of wavelet methods. This is followed by contributions from the most prominent researchers in the field, giving the reader a complete survey of the use of wavelets in biomedical engineering.

The book consists of four main sections:

• Wavelet Transform: Theory and Implementation
• Wavelets in Medical Imaging and Tomography
• Wavelets and Biomedical Signal Processing
• Wavelets and Mathematical Models in Biology

In this paper, we present an overview of the various uses of the wavelet transform (WT) in medicine and biology. We start by describing the wavelet properties that are the most important for biomedical applications. In particular, we provide an interpretation of the continuous WT as a prewhitening multi-scale matched filter. We also briefly indicate the analogy between the WT and some of the biological processing that occurs in the early components of the auditory and visual system. We then review the uses of the WT for the analysis of one-dimensional physiological signals obtained by phonocardiography, electrocardiography (ECG), and electroencephalography (EEG), including evoked response potentials. Next, we provide a survey of recent wavelet developments in medical imaging. These include biomedical image processing algorithms (e.g., noise reduction, image enhancement, and detection of microcalcifications in mammograms); image reconstruction and acquisition schemes (tomography, and magnetic resonance imaging (MRI)); and multiresolution methods for the registration and statistical analysis of functional images of the brain (positron emission tomography (PET), and functional MRI). In each case, we provide the reader with some general background information and a brief explanation of how the methods work. The paper also includes an extensive bibliography.

Le traitement des images médicales a pu être fortement amélioré et accéléré grâce à des fonctions mathématiques appelées splines. Michael Unser a apporté une contribution essentielle dans ce secteur, tant sur le plan de la théorie que des applications.

This chapter presents a survey of interpolation and resampling techniques in the context of exact, separable interpolation of regularly sampled data. In this context, the traditional view of interpolation is to represent an arbitrary continuous function as a discrete sum of weighted and shifted synthesis functions—in other words, a mixed convolution equation. An important issue is the choice of adequate synthesis functions that satisfy interpolation properties. Examples of finite-support ones are the square pulse (nearest-neighbor interpolation), the hat function (linear interpolation), the cubic Keys' function, and various truncated or windowed versions of the sinc function. On the other hand, splines provide examples of infinite-support interpolation functions that can be realized exactly at a finite, surprisingly small computational cost. We discuss implementation issues and illustrate the performance of each synthesis function. We also highlight several artifacts that may arise when performing interpolation, such as ringing, aliasing, blocking and blurring. We explain why the approximation order inherent in the synthesis function is important to limit these interpolation artifacts, which motivates the use of splines as a tunable way to keep them in check without any significant cost penalty.

The goals of this article are three-fold:

• To provide a tutorial on splines that is geared to a signal processing audience.
• To gather all their important properties, and to provide an overview of the mathematical and computational tools available; i.e., a road map for the practitioner with references to the appropriate literature.
• To review the primary applications of splines in signal and image processing.

For the first time, the field's leading international experts have come together to produce a complete guide to wavelet transform applications in medicine and biology. This book provides guidelines for all those interested in learning about waveletes and their applications to biomedical problems.

The introductory material is written for non-experts and includes basic discussions of the theoretical and practical foundations of wavelet methods. This is followed by contributions from the most prominent researchers in the field, giving the reader a complete survey of the use of wavelets in biomedical engineering.

The book consists of four main sections:

• Wavelet Transform: Theory and Implementation
• Wavelets in Medical Imaging and Tomography
• Wavelets and Biomedical Signal Processing
• Wavelets and Mathematical Models in Biology

In this paper, we present an overview of the various uses of the wavelet transform (WT) in medicine and biology. We start by describing the wavelet properties that are the most important for biomedical applications. In particular, we provide an interpretation of the continuous WT as a prewhitening multi-scale matched filter. We also briefly indicate the analogy between the WT and some of the biological processing that occurs in the early components of the auditory and visual system. We then review the uses of the WT for the analysis of one-dimensional physiological signals obtained by phonocardiography, electrocardiography (ECG), and electroencephalography (EEG), including evoked response potentials. Next, we provide a survey of recent wavelet developments in medical imaging. These include biomedical image processing algorithms (e.g., noise reduction, image enhancement, and detection of microcalcifications in mammograms); image reconstruction and acquisition schemes (tomography, and magnetic resonance imaging (MRI)); and multiresolution methods for the registration and statistical analysis of functional images of the brain (positron emission tomography (PET), and functional MRI). In each case, we provide the reader with some general background information and a brief explanation of how the methods work. The paper also includes an extensive bibliography.