Student Projects
Courses
460 projects

Improving Optimization Algorithms for Image Reconstruction in Ptychography Phase Retrieval
Supervisors: Zhiyuan Hu, Jonathan Dong

Sampling from Learned Regularizers
Supervisors: Stanislas Ducotterd, Youssef Haouchat

Likelihoods for Hawkes Processes
Supervisors: Vincent Guillemet
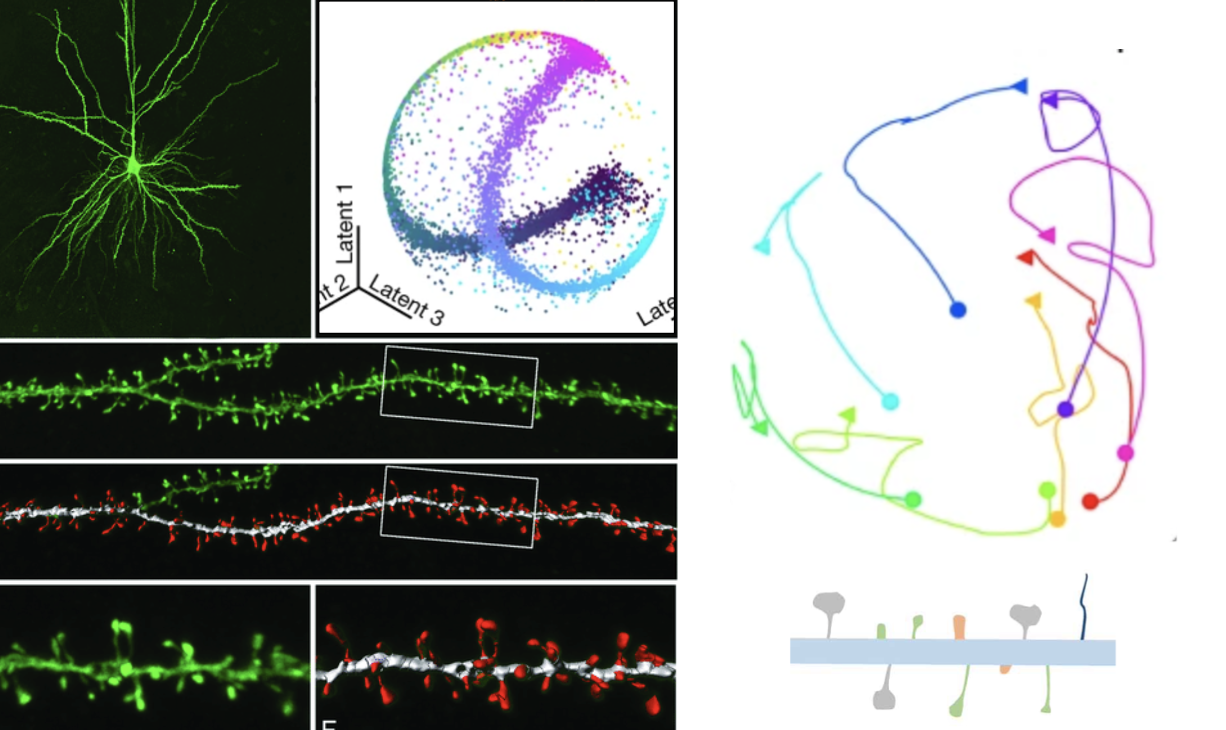
Analysis of dendritic spine changes using deep-learning encoding in a latent space
Supervisors: Aleix Boquet I Pujadas, Daniel Sage
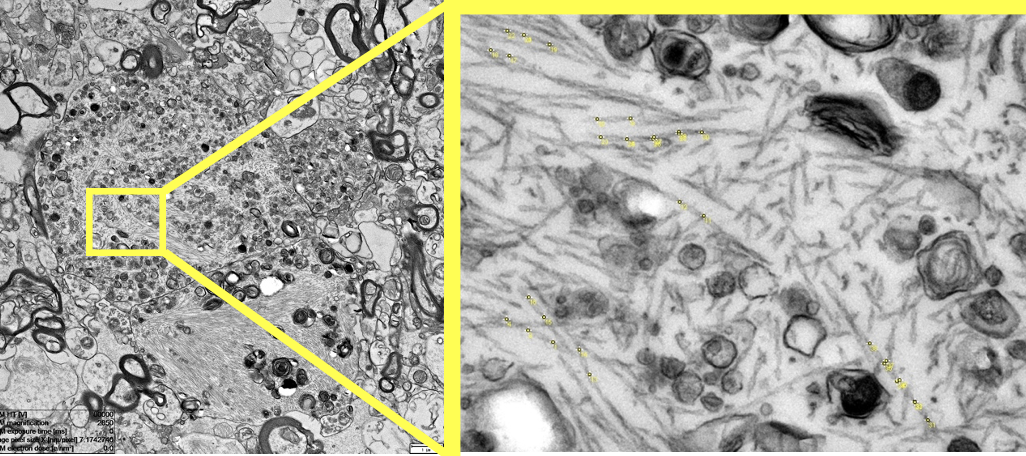
Automated image analysis of tau fibrils in the human Alzheimer's disease brain
Supervisors: Daniel Sage, Daniel Stähli

Discretization of Non-Uniform Sampling Problems with Exponential Splines
Aman Rishal Chemmala
Supervisors: Vincent Guillemet, Bassam El Rawas

Inverse Problems with ℓ1 Regularization: Extreme Points of the Regularization Polytope and Analysis vs Synthesis Formulations
Niels Rigaud
Supervisors: Bassam El Rawas, Martin Zach
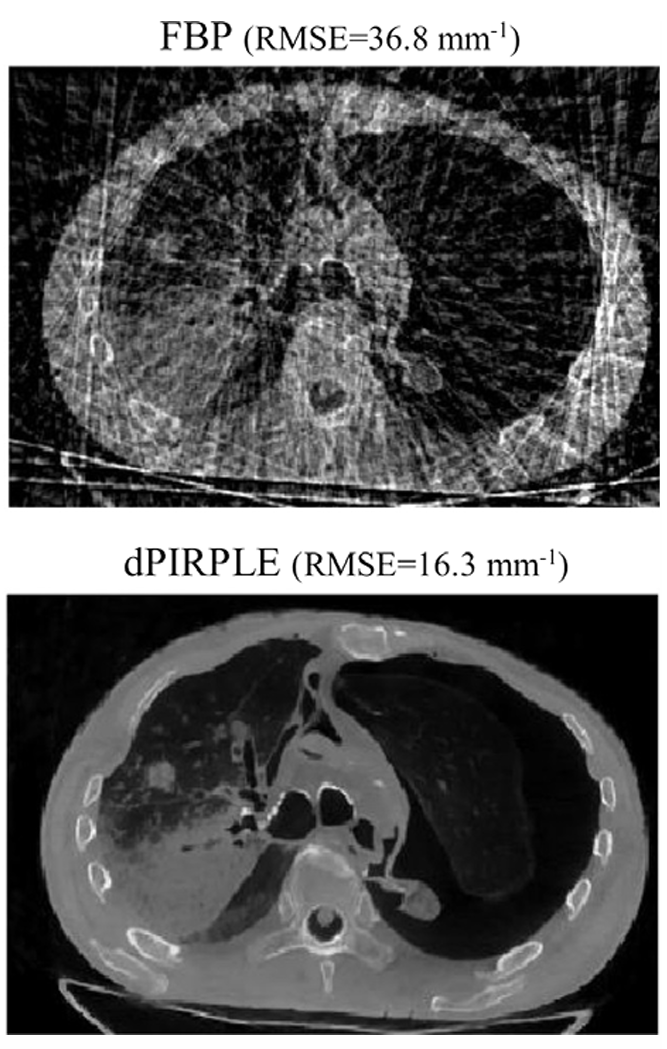
Tensor-Product-Based Regularization for Inverse Problems in Tomography
Supervisors: Vincent Guillemet, Youssef Haouchat
Diffusion Models for Magnetic Resonance Imaging Reconstruction
Angel Zenteno
Supervisors: Thomas Yu, Gian Franco Piredda, Mehrsa Pourya
SubjectSparse Unrolled Auto-Encoders for Interpretable Analysis of Neural Data
Valérie Costa
Supervisors: Bahareh Tolooshams, Sara Matias, Stanislas Ducotterd
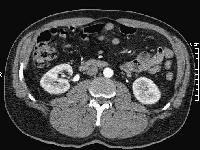
SubjectPrediction and survival analysis of ovarian cancer through multimodal fusion of radiomic and multiomic data.
Supervisors: Stéphanie Nougaret, Charles Berger, Jonathan Dong
SubjectPenalized Maximum Likelihood Approach for Deconvolution of Microscopy with Learned Convex Regularizer
Estelle Baup
Supervisors: Stanislas Ducotterd, Mehrsa Pourya
SubjectFrom PDE to Cell Imaging: A Multiresolution Framework for Fourier Ptychography
Efe Tarhan
Supervisors: Jonathan Dong, Vincent Guillemet
SubjectGenerating of Point-Spread Function for Advanced Imaging Microscopy in Python
Supervisors: Jonathan Dong, Vasiliki Stergiopoulou , Yan Liu and Daniel Sage
SubjectLight fluence modeling in photoacoustic imaging
Alexis-Darren Salathé
Supervisors: Jonathan Dong, Yan Liu
SubjectImage Processing Methods for Extracting Insights of IMAJ / UNESCO Drawing Database
Supervisors: Julien Fageot, Daniel Sage
SubjectMultigrid Solver For Non-Uniform Sampling With TV Regularization
Louis Grosse
Supervisors: Mehrsa Pourya, Vincent Guillemet
SubjectStylized approximations of curves and of 1-dimensional manifolds using splines
Bassam El Rawas
Supervisors: Vincent Guillemet
SubjectCharacterization of myelin structure using image analysis techniques
Raphaëlle Hartwig
Supervisors: Daniel Sage, Marta Di Fabrizio
SubjectPhotobleaching Correction using Self-Supervised Deep-Learning Methods in Fluorescence Microscopy
Louis Litzler-Italia
Supervisors: Stanislas Ducotterd, Daniel Sage
SubjectGeometry of Images: A War Between Fastness and Expressiveness
Supervisors: Vincent Guillemet, Mehrsa Pourya
SubjectImplicit Neural Representations for Denoising
Melchior Carrier
Supervisors: Stanislas Ducotterd, Rahul Parhi
SubjectNovel reconstruction in photoacoustic imaging
Jonathan Chuah Wen Jie
Supervisors: Yan Liu, Jonathan Dong
SubjectAnomaly detection in 4D flow MRI
Lavinia Schlyter
Supervisors: Jeremy Tan, Ender Konukoglu, Aleix Boquet-Pujadas
SubjectInvestigating Orthogonal Convolutions for Denoising
Valérie Costa
Supervisors: Stanislas Ducotterd, Sebastian Neumayer, Alexis Goujon
SubjectLearning of Continuous and Piecewise-linear Functions by the Multigrid Algorithm
Kamyar Rajabalifardi (Online Collaboration)
Supervisors: Mehrsa Pourya, Michael Unser
SubjectApproximation Theory with Exponential Splines
Bassam El Rawas
Supervisors: Rahul Parhi
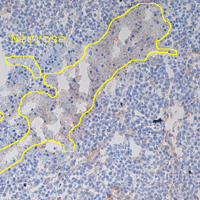
SubjectMachine Learning for Bone Marrow Histopathology
Zhu Zhihan
Supervisors: Daniel Sage, Rita Sarkis
SubjectAdvanced machine learning for probability density estimation
Supervisors: Aleix Boquet-Pujadas, , Michael Unser
SubjectGlacial Motion
Lucas Mutschler
Supervisors: Alexis Goujon, Daniel Sage
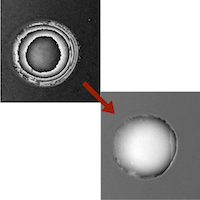
SubjectFast Structured Illumination Microscopy by Reducing the Number of Images Required
Alejandro Nogueron Aramburu
Supervisors: Daniel Sage, Emmanuel Soubies, Michael Unser
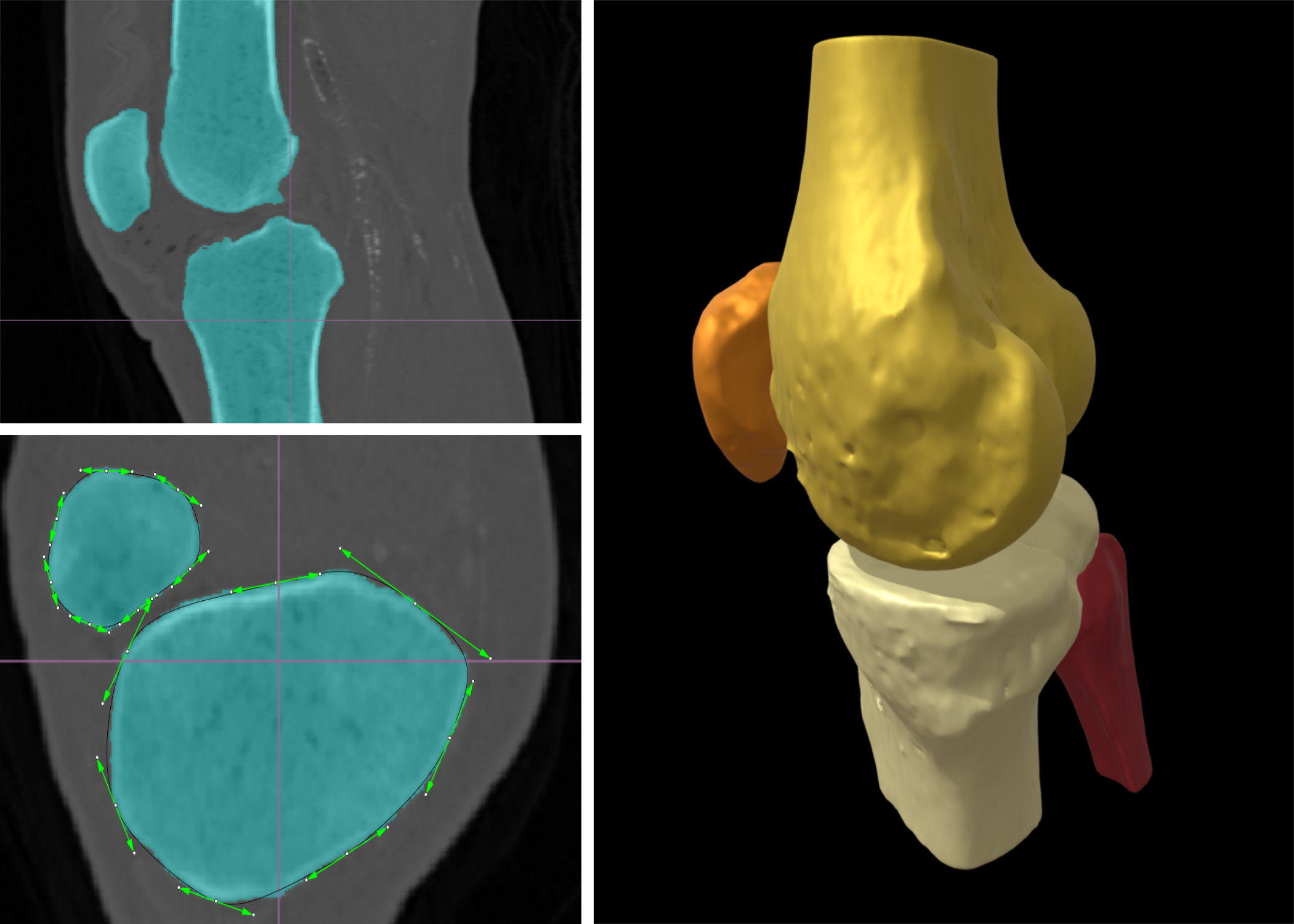
SubjectAutomatic bone segmentation with active parametric contour in CT images
Charles Berger
Supervisors: Daniel Sage, Pablo Garcia-Amorena
SubjectPosterior integrals with MCMC for Bayesian tests
Maxime Perret
Supervisors: Aleix Boquet-Pujadas, Pakshal Bohra, Michael Unser
SubjectAsymptotic stability analysis of Echo-State Networks
Erik Bengt Börve
Supervisors: Jonathan Dong, Michael Unser
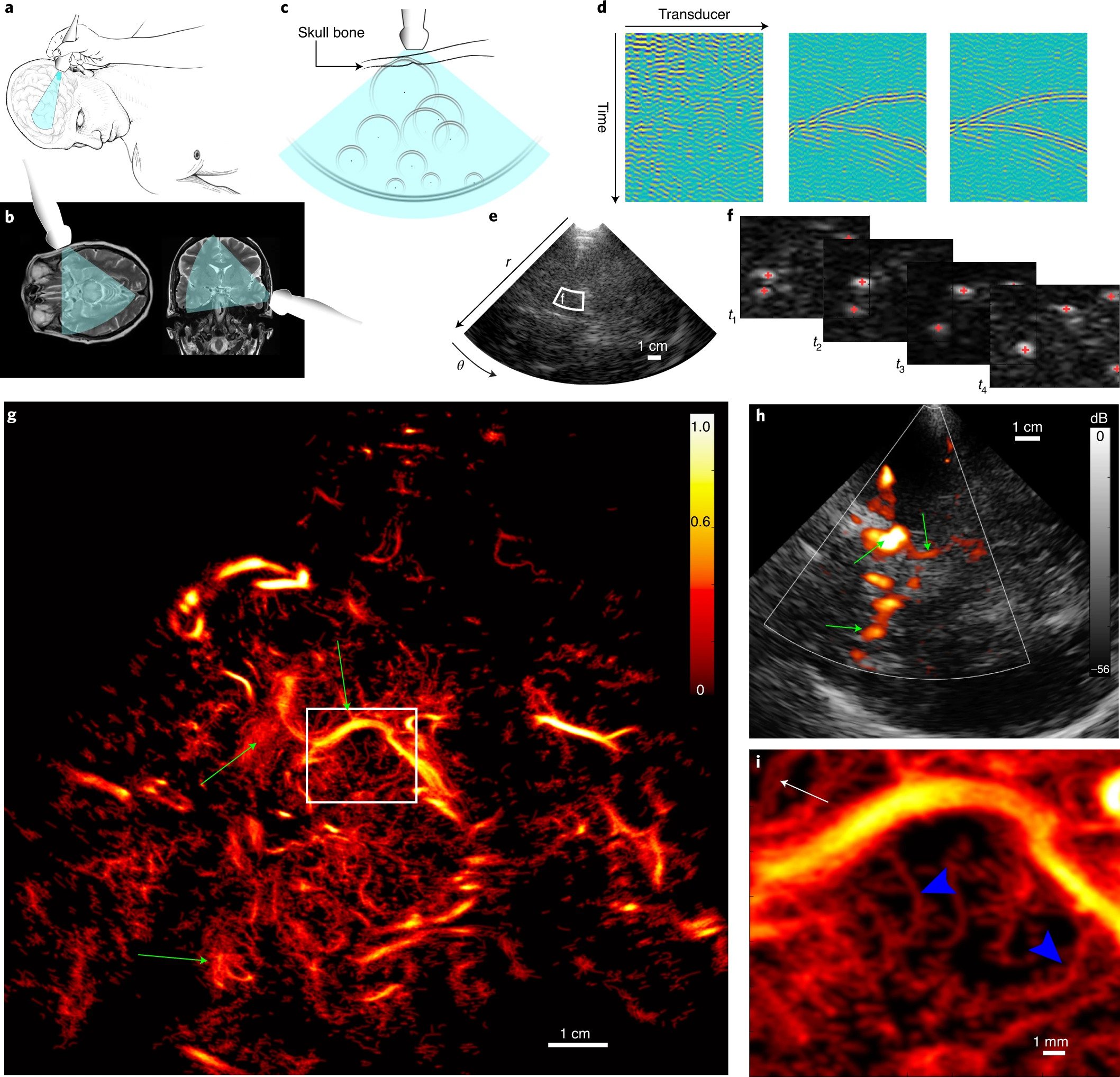
SubjectSpline-based sub-pixel localization of microbubbles for ultrafast ultrasound imaging of the brain vasculature
Malo Simondin
Supervisors: Thomas Debarre, Michael Unser, Dimitris Perdios
SubjectLearning sparse continuous and piecewise-linear functions for 3-dimensional data
Konstantin Sopov
Supervisors: Mehrsa Pourya, Michael Unser
SubjectSignal analysis of tree rings patterns in dendrochronological and forest ecosystem studies based on high resolution X-ray computed tomography (micro-CT) images
Charlotte Sertic
Supervisors: Philippe Thévenaz, Michael Unser
SubjectPerturbative Phase Retrieval
Kuan-Chen Shen
Supervisors: Jonathan Dong, Michael Unser
SubjectImage-based quantification of cell blebbing
Eugénie Demeure
Supervisors: Daniel Sage, Michael Unser
SubjectProximal Operators for Nonnegative Inverse Problems
Alejandro Noguerón Aramburu
Supervisors: Pol del Aguila Pla, Michael Unser
SubjectDeep learning for 3D particle field imaging
Margain Paul René Bertrand
Supervisors: Thanh-An Pham, Michael Unser
SubjectUsing regularization to reduce the number of projection angles in optical projection tomography
Aiday Marlen
Supervisors: Yan Liu, Michael Unser, Thanh-An Pham, thanh-an.pham@epfl.ch
SubjectEffect of Simple Operations on the Linear Regions of Continuous Piecewise Linear Functions
Haojun Zhu
Supervisors: Alexis Goujon, Michael Unser, Shayan Aziznejad
SubjectLightweight Deep Models for Dynamic MRI
Mielonen Eelis Valtteri
Supervisors: Jaejun Yoo, Michael Unser
SubjectContinuous-domain multicomponent image reconstruction with mixed regularization
Benoit Knuchel
Supervisors: Thomas Debarre, Michael Unser, Shayan Aziznejad
SubjectDeep neural network for SIM super-resolution reconstruction with a reduced number of images
Kay Lächer
Supervisors: Daniel Sage, Michael Unser, Emmanuel Soubies
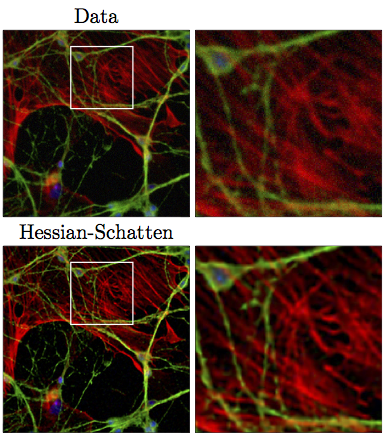
SubjectDifferentiable Approximation of Hessian-Schatten Regularization for Image Reconstruction
Mickael Gindroz
Supervisors: Thanh-An Pham, Michael Unser, Shayan Aziznejad
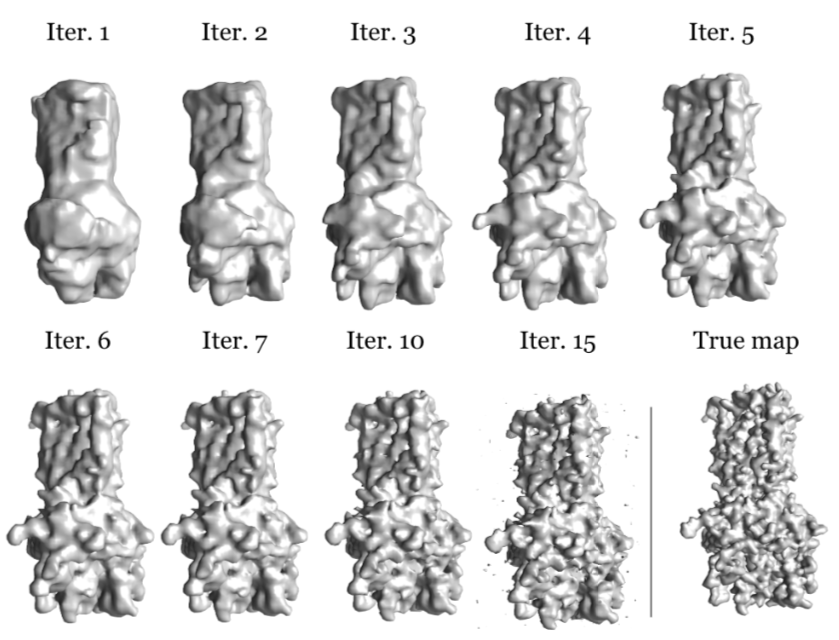
SubjectHigh-resolution reconstruction in single-particle cryo-EM with a multiscale joint refinement scheme
Paul Margain
Supervisors: Pakshal Bohra, Michael Unser, Thanh-An Pham, thanh-an.pham@epfl.ch
SubjectHomotopy Methods for Regularized Inverse Problems
Philippe Parisot
Supervisors: Thomas Debarre, Michael Unser
SubjectSlice-based Dictionary Learning for Computed Tomography
Louis-Nicolas Douce
Supervisors: Pakshal Bohra, Michael Unser, Thanh-An Pham
SubjectLearning Robust Neural Networks via Controlling their Lipschitz Regularity
Moulik Choraria
Supervisors: Jaejun Yoo, Michael Unser, Shayan Aziznejad
SubjectImage reconstruction for optical diffraction tomography
Mohamed Bahroun
Supervisors: Thanh-An Pham, Michael Unser
SubjectBenchmarking of Proximal Algorithms for Solving Regularized Inverse Problems
Malo Simondin
Supervisors: Thomas Debarre, Michael Unser
SubjectLipschitz Constrained Generative Adversarial Networks
Polina Proskura
Supervisors: Jaejun Yoo, Michael Unser, Joaquim Campos, joaquim.campos@epfl.ch, BM 4.141
SubjectAnalysis of tree rings patterns in dendrochronological and forest ecosystem studies
Malo Simondin
Supervisors: Philippe Thévenaz, Michael Unser, Pascal Turberg (EPFL ENAC IIC PIXE)
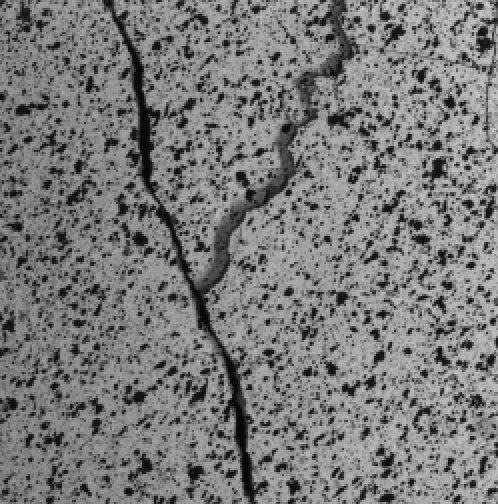
SubjectImage analysis algorithm for crack detection in walls
Rémy Dornier
Supervisors: Daniel Sage, Michael Unser, Katrin Beyer, Amir Rezaie (ENAC)
SubjectDeep Learning and Image Analysis to Distinguish Murine form Human cells (Prof C. Brisken)
Quentin Juppet
Supervisors: Daniel Sage, Michael Unser
SubjectReview and implementation of loss functions for image-to-image neural network
Alexandre Levy
Supervisors: Daniel Sage, Michael Unser, Jaejun Yoo
SubjectDynamic of cracks in wall based on analysis of image sequence
Emma Bouton-Bessac
Supervisors: Daniel Sage, Michael Unser, Amir Rezaie
SubjectGrowth of E. coli cells: simulation of images data to training of a neural network (Prof. McKinney)
Héloïse Monnet
Supervisors: Daniel Sage, Michael Unser
SubjectPhase Retrieval in the GlobalBioIm library
Benoît Pelisson
Supervisors: Jonathan Dong, Michael Unser
SubjectHigher-Order Regularization Methods for Supervised Learning
Joaquim Campos
Supervisors: Shayan Aziznejad, Michael Unser
SubjectGenerating Sparse Stochastic Processes
Leello Dadi
Supervisors: Shayan Aziznejad, Michael Unser
SubjectLearning the 3D structure of proteins with dictionary learning
Stefania Konstantinidi
Supervisors: Laurène Donati, Michael Unser
SubjectPhase Unwrapping with Deep Learning
Jérome Savary
Supervisors: Thanh-An Pham, Michael Unser, Kyong Hwan Jin
SubjectBenchmarking of numerical methods for solving inverse problems
Zhiwei Huang
Supervisors: Pakshal Bohra, Michael Unser, Emmanuel Soubies
SubjectImage analysis plugin to monitor the growth of lithium particles in TEM images (INE lab, Tileli Vasiliki)
Shad Ali Durussel
Supervisors: Daniel Sage, Michael Unser, Laurène Donati
SubjectReconstruction of autofluorescence optical projection tomography
Thomas Ramseier
Supervisors: Mike McCann, Michael Unser, Thanh-An Pham
SubjectAn off-the-grid algorithm in ImageJ for 3D single-molecule localization microscopy
Amandine Evard
Supervisors: Thanh-An Pham, Michael Unser, Quentin Denoyelle
SubjectLearning Spline-based activations for very deep learning
Joaquim Campos
Supervisors: Harshit Gupta, Michael Unser
SubjectImplementing Deep-learning-based iterative algorithm to solve inverse problem of MRI
Huy Thong Phan
Supervisors: Harshit Gupta, Michael Unser, Than-an Pham
SubjectTiming correction for slow-scanning biomedical imaging devices
Luca Fetz
Supervisors: Thomas Debarre, Michael Unser, Thanh-An Pham
SubjectSimulating realistic synthetic data sets for developing a self-driving microscope
Robin Lang
Supervisors: Daniel Sage, Michael Unser, Juliette Griffié and Suliana Manley LEB EPFL
SubjectDictionary Learning for Limited Angle Computed Tomography
Clélie De Witasse
Supervisors: Thanh-An Pham, Michael Unser, Pakshal Bohra, pakshal.bohra@epfl.ch
SubjectDeep Learning for Angle Estimation in Cryo-EM
Jelena Bancac
Supervisors: Laurène Donati, Michael Unser, Michaël Defferrard (LTS2)
SubjectAn off-the-grid algorithm in ImageJ for 3D single-molecule localization microscopy
Elias Gajo
Supervisors: Quentin Denoyelle, Michael Unser, Thanh-An Pham
SubjectQuantifying cell cycle-gated expression of transcription factors by machine learning on fluorescence microscopy data (Prof. D. Suter)
Mai Yuanfei
Supervisors: Anonymous, Daniel Sage, David Suter
SubjectTracking animal behavior in neuroimaging studies
Julien Rüegg
Supervisors: Virginie Uhlmann, Michael Unser
SubjectSparse Signal Reconstruction using Variational Methods with Fractional Derivatives
Stefan Stojanovic
Supervisors: Thomas Debarre, Michael Unser, Julien Fageot
SubjectOptimal Configurations for Parallel-Beam Computed Tomography
Martial Bernard-Michel
Supervisors: Laurène Donati, Michael Unser
SubjectTwo dimensional SIM reconstruction from 4 images
Christophe Muller
Supervisors: Emmanuel Soubies, Michael Unser
SubjectSteerable filters as imaging biomarkers for precision medicine
Mickaël Salamin
Supervisors: Adrien Depeursinge, Michael Unser, Prof. Xavier Montet, HUG
SubjectDeep convolutional neural networks for precision medicine
Roser Viñals
Supervisors: Adrien Depeursinge, Michael Unser, Prof. Xavier Montet (HUG), Dr. Kyong Jin
SubjectWeb tools for image processing and for super-resolution microscopy visualisation
Robin Lang
Supervisors: Daniel Sage, Michael Unser
SubjectColor Thread-Toning
Icíar Lloréns Jover
Supervisors: Mike McCann, Michael Unser
SubjectImproving depth-of-field by deconvolution
Cédric Schumacher
Supervisors: Emmanuel Soubies, Michael Unser, Thanh-An Pham
SubjectMonitoring plant phenotyping by time-lapse video
Arthur Benzaquin
Supervisors: Daniel Sage, Michael Unser, Prof. Colin Jones
SubjectInteractive B-spline demo running in a web browser
Robin Lang
Supervisors: Daniel Schmitter, Michael Unser
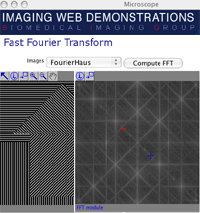
SubjectDidactic demonstrations for image-processing courses in HTML5 / Javascript
Cyril Favre
Supervisors: Daniel Sage, Michael Unser
SubjectDeep Learning for Image Inpainting
Arbani Amr
Supervisors: Kyong Jin, Michael Unser
Subject3D Steerable Filter Learning for Efficient Volumetric Image Analysis
Camille Boymond
Supervisors: Adrien Depeursinge, Michael Unser, Julien Fageot, julien.fageot@epfl.ch, BM 4.139, Tel: 021 693 3701
SubjectDesign of optimal 2D-steerable filters: theory and implementation
Benjamin Beck
Supervisors: Julien Fageot, Michael Unser, Adrien Depeursinge
SubjectLearning Approach for Image Restoration
Carlos Malanche
Supervisors: Ha Nguyen, Michael Unser
SubjectA study of the tip detection problem
Alexandre Cherqui
Supervisors: Virginie Uhlmann, Michael Unser
SubjectB-spline implementation to find the solution of continuous domain total-variation minimization problem
Thomas Debarre
Supervisors: Harshit Gupta, Michael Unser
SubjectRegion of Interest Computed Tomography
Laura Vilaclara
Supervisors: Mike McCann, Michael Unser
SubjectDeep Learning for Medical Imaging (MRI)
Christophe Windler
Supervisors: Kyong Jin, Michael Unser
SubjectBuilding a Theory for Hermite L-splines
Julien Rüegg
Supervisors: Julien Fageot, Michael Unser, Virginie Uhlmann, virginie.uhlmann@epfl.ch, BM 4.142, Tel: 021 693 1136
SubjectSuper-resolution imaging using Deep-Learning
Clémentine Aguet
Supervisors: Emmanuel Soubies, Michael Unser, Kyong Jin, kyong.jin@epfl.ch, BM 4.135, Tel: 021 693 5189
SubjectResolution improvement by 3D multiview reconstruction in SPIM imaging
Katarina Lichardova
Supervisors: Denis Fortun, Michael Unser, Ferreol Soulez
SubjectFramework for pixel classification system in time-lapse microscopy images
Julien Marengo
Supervisors: Daniel Sage, Michael Unser, Kyong Jin, Anaïs Badoual
SubjectSparse steerable textons
Jeremy Casorso
Supervisors: Adrien Depeursinge, Michael Unser, Daniel Schmitter, Julien Fageot
SubjectActive Contour for Jointly Segmentation of Multiple Cells
Aymeric Galan
Supervisors: Anaïs Badoual, Michael Unser, Daniel sage, daniel.sage@epfl.ch
SubjectRotation axis estimation for parallel-beam X-ray CT
Claire Stoffel
Supervisors: Mike McCann, Michael Unser
SubjectSemi-blind reconstruction for Structured Illumination microscopy
Rémy Gardier
Supervisors: Emmanuel Soubies, Michael Unser, Laurène Donati, laurene.donati@epfl.ch
SubjectRestoring axial resolution using a 2D/3D deep convolution neuronal network
Joey Zenhäusern
Supervisors: Daniel Sage, Michael Unser, Kyong Jin, kyong.jin@epfl.ch
SubjectDeep neural networks: learning with splines
Arnaud Pannatier
Supervisors: Anaïs Badoual, Michael Unser, Shayan Aziznejad
SubjectQuantification of fiber-like structures in time-lapse fluorescence microscopy images
Florian Poma
Supervisors: Daniel Sage, Michael Unser
SubjectImplementation of scalable detectors in 2D/3D
Robin Weiskopf
Supervisors: Zsuzsanna Puspöki, Michael Unser
SubjectA theoretical study of steerable homogeneous operators
Lilian Besson
Supervisors: Julien Fageot, Michael Unser
SubjectDeep Convolutional Neural Networks for Texture Classification
Thibault Groueix
Supervisors: Adrien Depeursinge, Michael Unser
SubjectAnalysis of cortical structures from 3D live imaging of C. elegans embryos
Jean Frédéric Haizmann
Supervisors: Daniel Sage, Michael Unser, Pierre Gönczy
SubjectLearning-Based Attenuation of the Noise of a Speech Recording
Valentin Oreiller
Supervisors: Denis Fortun, Michael Unser
SubjectData Augmentation for Deep Learning
Matthieu Cotting
Supervisors: Anaïs Badoual, Michael Unser, Daniel Sage
SubjectCompressibility of sparse stochastic processes
Shayan Aziznejad
Supervisors: Julien Fageot, Michael Unser
SubjectTexture Snake for Tumor Grading
Yann Perret
Supervisors: Anaïs Badoual, Michael Unser, Adrien Depeursinge
SubjectSimultaneous Phase and Amplitude Extraction in X-ray Computed Tomography
Pedro Roberto
Supervisors: Masih Nilchian, Michael Unser
Subject3D Steerable Filter for Foam Junction Detection
Benjamin Beck
Supervisors: Adrien Depeursinge, Michael Unser, Zsuzsanna Püspöki
SubjectJava optimization package development
Sahar Hanna
Supervisors: Zsuzsanna Puspöki, Michael Unser
SubjectDeconvolution of multi-spectral multi-frame astrophysical images
Michal Tyszkiewicz
Supervisors: Ferréol Soulez, Michael Unser
SubjectQuantifying cell deformation with optical flow in time-resolved super-resolution
Colin Darbellay
Supervisors: Denis Fortun, Michael Unser, Theo Lasser
SubjectAnalysis of cortical structures from 3D live imaging of C. elegans embryos
Baptiste Sottas
Supervisors: Daniel Sage, Michael Unser
SubjectVariational approaches for optical flow estimation
Christopher Finelli
Supervisors: Emrah Bostan, Michael Unser, Denis Fortun, denis.fortun@epfl.ch, BM 4.135, Tel: 31219
SubjectRegularity of Sparse Stochastic Processes
Alireza Fallah
Supervisors: Julien Fageot, Michael Unser
SubjectImage Calibration for Super-resolved Structured Illumination Microscopy (SIM)
Roland Nussbaumer
Supervisors: Daniel Sage, Michael Unser, 1) Ning Chu ning.chu@epfl.ch BM 4.141 Tel 021 693 51 43
SubjectReconstruction of a 3D map of the refractive index from digital holography microscopy data
Sander Kromwijk
Supervisors: Ulugbek Kamilov, Michael Unser
SubjectSelf-Similar Image Doubling by Hallucinating the Lazy Wavelet
Christopher Finelli
Supervisors: Philippe Thévenaz, Michael Unser
SubjectSegmentation of cardiac images in 3D MRI
Christophe Gaudet-Blavignac
Supervisors: Daniel Schmitter, Michael Unser, Davide Piccini (CVMR, CIBM-Siemens)
SubjectAnnulus detection method with active contours
Timothée Bronner
Supervisors: Daniel Sage, Michael Unser
SubjectTracking Keratinocytes in co-culture
Arik Girsault
Supervisors: Virginie Uhlmann, Michael Unser, Daniel Sage, daniel.sage@epfl.ch, BM 4.135, Tel: 021 693 51 89
SubjectTexture segmentation based on steerable wavelets
Vasileios Angelopoulos
Supervisors: Martin Storath, Michael Unser, Adrien Depeursinge
SubjectSuper-resolution Image Reconstruction for Structured Illumination Microscopy (SIM) as ImageJ Plugin
Roland Nussbaumer
Supervisors: Daniel Sage, Michael Unser, 1) Ning Chu ning.chu@epfl.ch BM 4.141 Tel 021 693 51 43
SubjectQuantification of the host pathogen interactions by image analysis (II)
Ariane Kaeppeli
Supervisors: Daniel Sage, Michael Unser, Matthieu Delincé
SubjectMaya (or Blender) plugin development for spline surface deformation
Romain Degoul
Supervisors: Daniel Schmitter, Michael Unser
SubjectCorner Detection based on PDE Methods
Vermot Bertrand
Supervisors: Virginie Uhlmann, Michael Unser, Julien Fageot, julien.fageot@epfl.ch, BM 4.139, Tel: 021 693 3701
SubjectDesign of active contour models using NURBS
rimmiryam.chaabouni@epfl.ch
Supervisors: Virginie Uhlmann, Michael Unser, Daniel Schmitter, daniel.schmitter@epfl.ch, Julien Fageot, julien.fageot@epfl.ch
SubjectInteractive image segmentation based on the Potts model
Vasileios Angelopoulos
Supervisors: Martin Storath, Michael Unser
SubjectPhysics-based active contour energy to prevent twisting of parametric spline snakes
Araz Yaqubov
Supervisors: Daniel Schmitter, Michael Unser, Pedram Pad (pedram.pad@epfl.ch), Anaïs Badoual (anais.badoual@epfl.ch)
SubjectMeasuring ocular blood flow using steerable Hessian wavelets
Blaise Robert
Supervisors: Adrien Depeursinge, Michael Unser, Prof Martial Geiser, HES-SO Sion
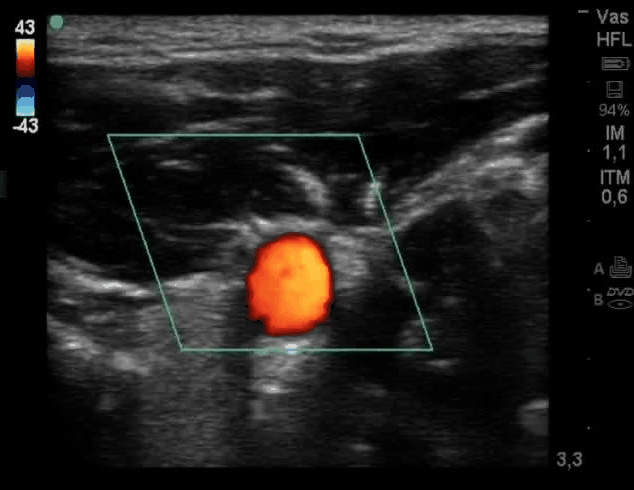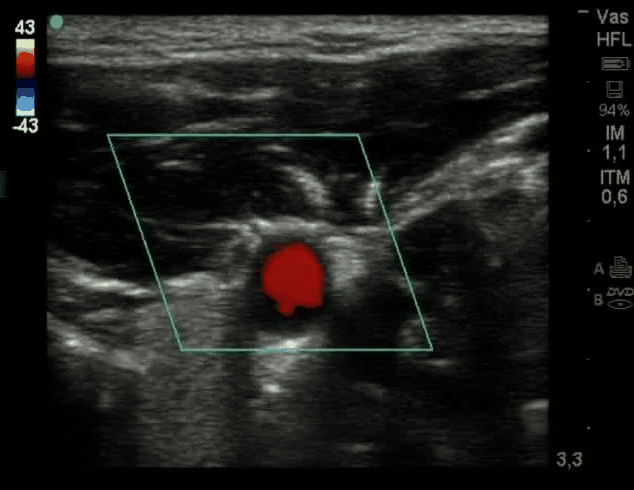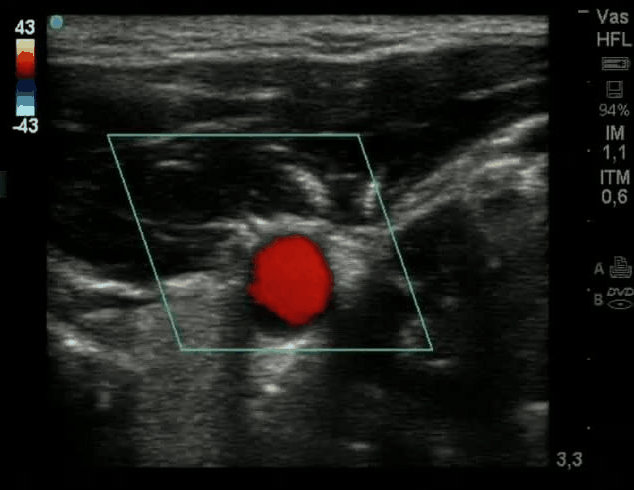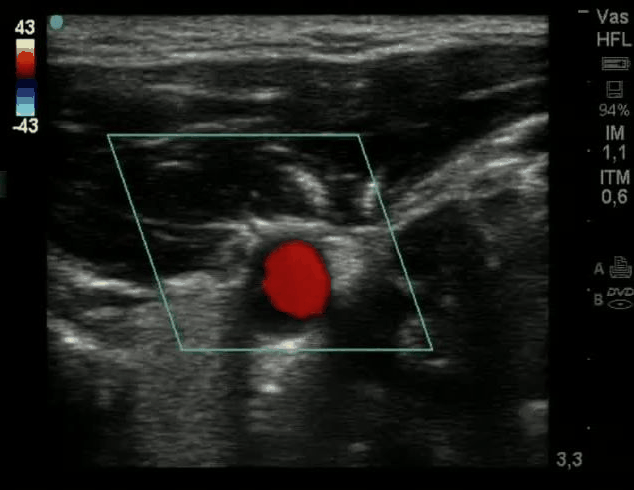
SubjectSegmentation of Doppler ultrasound images for monitoring the blood flow
Brune Bastide and Axel Vandebrouck
Supervisors: Anaïs Badoual, Michael Unser, Daniel Sage, Raoul Schorer
SubjectParametric shape representation using spline-based basis functions
Pablo Garcia-Amorena
Supervisors: Daniel Schmitter, Michael Unser
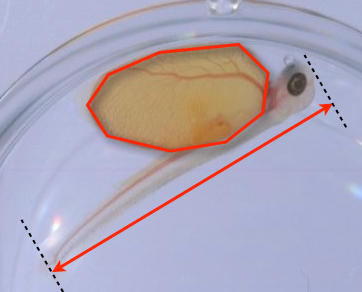
SubjectMorphometric measurement of larvae of fish by image analysis
Luc Girod
Supervisors: Daniel Sage, Michael Unser
SubjectSpatio-temporal Analysis of Biomedical Images Using Active Cells
Julien Jacquemot and Clément Marti
Supervisors: Ricard Delgado-Gonzalo, Michael Unser
SubjectScalable wavelet on biological images
Lucio Genini
Supervisors: Zsuzsanna Puspöki, Michael Unser, John-Paul Ward, Daniel Sage
SubjectDetection and enhancement of blood flow in a video
Lucas Vandroux
Supervisors: Pedram Pad, Michael Unser, Virginie Uhlmann, virginie.uhlmann@epfl.ch, BM 4.142, Tel: 021 693 1136
SubjectRefining leg-movement extraction in high-speed videos of insect locomotion
Lucas Amoudruz
Supervisors: Virginie Uhlmann, Michael Unser, Pavan Ramdya, pavan.ramdya@epfl.ch, ELE 130, Tel: 021 693 69
SubjectModelling mycobacteria behavior in time-lapse microscopy images
Laurène Donati
Supervisors: Virginie Uhlmann, Michael Unser
SubjectFinding strong gravitational lenses using the ESA Euclid space telescope
Emmanuel Girardin
Supervisors: Zsuzsanna Puspöki, Michael Unser
SubjectDesigning Tip-Detectors
Pritish Chakravarty
Supervisors: Virginie Uhlmann, Michael Unser, Zsuzsanna Püspöki, zsuzsanna.puspoki@epfl.ch, BM 4.139, Tel: 021 693 51 57
SubjectIdentification of Physical Properties Obtained at Nanometer Scale by Combining Infrared Spectroscopy with Atomic-Force Microscopy
Stéphanie Becker
Supervisors: Philippe Thévenaz, Michael Unser
Subject3D microscopy deconvolution on GPU
Sander Kromwijk
Supervisors: Stamatis Lefkimmiatis, Michael Unser
SubjectInteractive demo for Signals & Systems course
Mamoun Benkirane
Supervisors: Ulugbek Kamilov, Michael Unser
SubjectClassifying galaxy type using the ESA Euclid space telescope
Christopher Finelli
Supervisors: Daniel Schmitter, Michael Unser, Virginie Uhlmann, virginie.uhlmann@epfl.ch, BM 4.142, Tel: 021 693 1136
SubjectTracking flagella undulations in microscopy images
Amicie De Pierrefeu
Supervisors: Daniel Sage, Michael Unser, Daniel Sage, daniel.sage@epfl.ch, BM 4.135, Tel: 021 693 51 89
SubjectDeconvolution in biomicroscopy
Charlotte Juillard
Supervisors: Daniel Sage, Michael Unser
SubjectQuantification of the host pathogen interactions by image analysis
Ariane Kaeppeli
Supervisors: Daniel Sage, Michael Unser
SubjectJunction detection in biomedical micrographs
Kilian Thomas
Supervisors: Zsuzsanna Puspöki, Michael Unser, Julien Fageot
SubjectFlow field enhancement with divergence-free wavelets
Florence Gavin
Supervisors: Emrah Bostan, Michael Unser, Emrah Bostan, emrah.bostan@epfl.ch, BM 4.140, Tel: 35142
SubjectInvestigation of the multiscale (wavelet-domain) statistics of natural and biomedical images
Thomas Pumir de Louvigny
Supervisors: Julien Fageot, Michael Unser
SubjectSegmentation and tracking of growing colony of mycobacteria
Olivia Mariani
Supervisors: Virginie Uhlmann, Michael Unser, Daniel Sage
SubjectAssessment of imaging performance in confocal fluorescence microscopy
Elia Ben Hamou and Edoardo D'Anna
Supervisors: Cédric Vonesch, Michael Unser
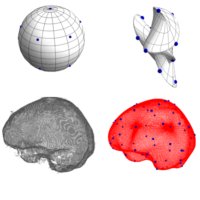
SubjectTotal Intracranial Volume Extraction on 3D MRI MP2RAGE Data
Daniel Schmitter
Supervisors: Ricard Delgado-Gonzalo, Michael Unser
SubjectA practical inverse problem approach for phase imaging
Emmanuel Froustey
Supervisors: Emrah Bostan, Michael Unser, Daniel Sage, daniel.sage@epfl.ch, BM 4.135, Tel: 021 693 51 89
SubjectObject Classification with Kinect
Julien Schwab
Supervisors: Ulugbek Kamilov, Michael Unser
SubjectOptical Flow Estimation under Sparsity Constraints
Emmanuel Froustey
Supervisors: Emrah Bostan, Michael Unser, Pouya D. Tafti, pouya.tafti@epfl.ch, BM 4.142
SubjectGPU accelerated 3D deconvolution
Christophe Zurn
Supervisors: Stamatis Lefkimmiatis, Michael Unser
SubjectSwallowing Human
Benjamin D'incau
Supervisors: Ricard Delgado-Gonzalo, Michael Unser, Daniel Sage
SubjectTracking leg movements in high-speed videos of insect locomotion
Loïc Perruchoud
Supervisors: Cédric Vonesch, Michael Unser
SubjectJava Application for the Easy Creation of an Art Catalogue
Thibault Priquel
Supervisors: Philippe Thévenaz, Michael Unser
SubjectApplet in Java for the Representation of Shapes Using Fourier Series
Lukas De Oliveira Prestes
Supervisors: Daniel Sage, Michael Unser
SubjectOptical Image Compression
Marcos Gonzalez Diego
Supervisors: bourquard, Michael Unser
SubjectThe double helix PSF: implementation and localization applications
Valentin Oreiller
Supervisors: Hagai Kirshner, Michael Unser
SubjectGuitar-tuner app for the iPhone
David Maksa
Supervisors: Cédric Vonesch, Michael Unser
SubjectCone Beam Differential Phase Contrast X-ray Computed Tomography
Simon-Pierre Génot
Supervisors: Masih Nilchian, Michael Unser
SubjectCoil Sensitivity Estimation for Parallel Magnetic Resonance Imaging
Pascal Bienz
Supervisors: Emrah Bostan, Michael Unser, Stamatis Lefkimmiatis, stamatis.lefkimmiatis@epfl.ch, BM 4.138, Tel: 351 36
SubjectActive Contour for the Detection of Coronary Artery in Ultrasonography
Shogo Hiramatsu
Supervisors: Ricard Delgado-Gonzalo, Michael Unser
SubjectTransport-of-intensity approach for quantitative phase imaging
David Nguyen
Supervisors: Emrah Bostan, Michael Unser, Daniel Sage, daniel.sage@epfl.ch, BM 4.135, Tel: 021 693 51 89
SubjectBounds for the MMSE of Estimation of Stable AR(1) Processes Embedded in Gaussian Noise
Seyed Mohsen Moosavi Dezfooli
Supervisors: Pedram Pad, Michael Unser
SubjectRepresentation of Stable AR(1) Processes with Partially Coupled Coefficients in Transform Domain
Mohamad Dia
Supervisors: Pedram Pad, Michael Unser
SubjectHigh-Throughput 3D Segmentation of Living Tissue
Julien Jacquemot and Clément Marti
Supervisors: Ricard Delgado-Gonzalo, Michael Unser
SubjectExtracting high-speed insect behavior at micrometer precision
Michael Rusterholz
Supervisors: Cédric Vonesch, Michael Unser
SubjectUsing Spline Normals to Render Marching Tetrahedra
Sascha Spiegl
Supervisors: Philippe Thévenaz, Michael Unser
SubjectArtifact reduction in phase-contrast X-ray imaging
Pascal Bienz
Supervisors: Masih Nilchian, Michael Unser
SubjectKinect (TM) control interface for 3D visualization
Stéphanie Falbriard
Supervisors: Ricard Delgado-Gonzalo, Michael Unser
SubjectIdentification of biomarkers in defocussed images
Frédéric Stauber
Supervisors: Cédric Vonesch, Michael Unser
SubjectImage inpainting with second-order diffusion
Philippe Favre
Supervisors: Stamatis Lefkimmiatis, Michael Unser, Aurélien Bourquard, aurelien.bourquard@epfl.ch, BM 4.138, Tel: 021 693 51 36
SubjectPhase Wrapping in X-ray Differential Phase-Contrast Tomography
Laurent Abouchar
Supervisors: Masih Nilchian, Michael Unser
SubjectSolving Inverse Problems with Sparsifying Transforms
Bugra Tekin
Supervisors: Ulugbek Kamilov, Michael Unser, Emrah Bostan, emrah.bostan@epfl.ch, BM 4.140
SubjectReconstruction of Signals from Sign Measurements
Ipek Baz
Supervisors: Ulugbek Kamilov, Michael Unser, Aurélien Bourquard, aurelien.bourquard@epfl.ch, BM 4.138, 021 693 5136
SubjectRadially-symmetric compactly-supported image modeling
Adrian Hauswirth
Supervisors: John Paul Ward, Michael Unser, Hagai Kirshner, hagai.kirshner@epfl.ch, BM 4142, Tel: 31136
SubjectCharacterization of G protein coupled receptors by image analysis
Chen Zhiwei
Supervisors: Daniel Sage, Michael Unser
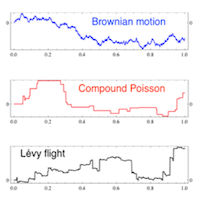
SubjectBiological Particles with Levy Motility
Adrien Rosselet
Supervisors: Pedram Pad, Michael Unser
SubjectDetection of the Wing Structure for the Systems Biology Drosophila Fly
Jesús Ayala Domínguez
Supervisors: Ricard Delgado-Gonzalo, Michael Unser, Thomas Schaffter, thomas.schaffter@epfl.ch, ELE 133
SubjectInvestigation of the multiscale (wavelet-domain) statistics of natural and biomedical images
Julien Fageot
Supervisors: Pouya Dehghani Tafti, Michael Unser
SubjectMulti-Scale Analysis of Non-Gaussian Innovation Models with First-Order Spatial Dependencies
Patrick Farnole
Supervisors: Pouya Dehghani Tafti, Michael Unser
SubjectVisible Human on the iPhone
Mohamed Amine Barhoumi
Supervisors: Philippe Thévenaz, Michael Unser
SubjectMonitoring the Point Spread Function (PSF) of a microscope for 3D life cell imaging
Philippe Hanhart
Supervisors: bourquard, Michael Unser, 1)Alessandra Griffa (Office: AI 0140, tel: 39629, email: alessandra.griffa@epfl.ch)
SubjectCell Segmentation with Coupled Active Contours
Hadrien Mottaz
Supervisors: Philippe Thévenaz, Michael Unser
SubjectTime-scaling, pitch-shifting of audio
Rafael Mosberger
Supervisors: Nicolas Chenouard, Michael Unser
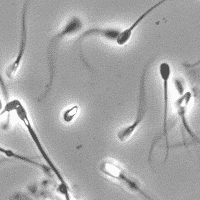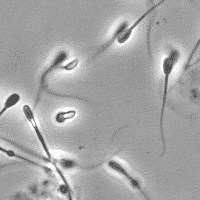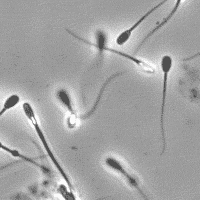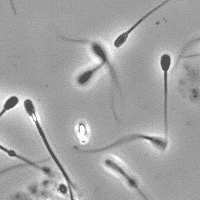
SubjectImage Analysis of the Motility of Spermatozoa
Martin Proença
Supervisors: Ricard Delgado-Gonzalo, Michael Unser
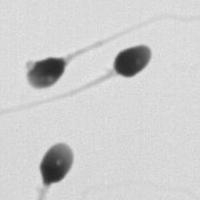
SubjectImage Analysis of the Morphology of a Spermatozoon
Raphaël Burgener
Supervisors: Nicolas Chenouard, Michael Unser
SubjectApplications of the monogenic image analysis
Virginie Uhlmann
Supervisors: Daniel Sage, Michael Unser
SubjectAnalytical Fourier samples of spline-defined regions for pMRI reconstruction phantoms
Laurent Lejeune
Supervisors: Guerquin-Kern Matthieu, Michael Unser
SubjectSpeedometer on the iPhone
David Bonzon
Supervisors: Philippe Thévenaz, Michael Unser
SubjectMedical Image Segmentation with Shape Priors
Samuel Garessus
Supervisors: Ricard Delgado-Gonzalo, Michael Unser
SubjectQuantitation of asymmetric mitosis by tracking the spindle poles using fluorescence images
Daniel Schmitter
Supervisors: Daniel Sage, Michael Unser
SubjectProcessing and analysis of biological images using the fast bilateral filter
Cléo Moulin
Supervisors: Masih Nilchian, Michael Unser, Daniel Sage
SubjectEstimation of the 3D structure in super-resolution fluorescence microscopy (PALM)
Patrizia Spoerri
Supervisors: Hagai Kirshner, Michael Unser, Daniel Sage (BM 4.135) tel 351 89
SubjectSpatiotemporal Segmentation of Migrating Cells in Fluorescence Microscopy
Florentin Marty
Supervisors: Ricard Delgado-Gonzalo, Michael Unser
SubjectReal-time stereo-matching using an adaptive bilateral filter
Oliver Akermann
Supervisors: Philippe Thévenaz, Michael Unser, Daniel Sage
SubjectPhotobleaching correction in fluorescence imaging (STED)
Abdolreza Madi
Supervisors: Stamatis Lefkimmiatis, Michael Unser, Daniel Sage
SubjectOptimal signal estimators for stable Levy processes
Patrick Farnole
Supervisors: Pouya Dehghani Tafti, Michael Unser
SubjectIdentification of Point Spread Function (PSF) aberrations using genetic algorithms
Jérémy Zogg
Supervisors: bourquard, Michael Unser
SubjectAccurate approximations for L1 image denoising
Clémentine Ouziel
Supervisors: bourquard, Michael Unser, Stamatis Lefkimmiatis, stamatis.lefkimmiatis@epfl.ch, BM 4.138, Tel: 351 36
SubjectReal-Time Registration of Visible and Thermal Network Cameras
Raphael Zaugg
Supervisors: Ricard Delgado-Gonzalo, Michael Unser
SubjectInteractive audio filter design application for the iPhone (TM)
Michael Rusterholz
Supervisors: Pouya Dehghani Tafti, Michael Unser
SubjectWhen the iPhone Meets Fourier
Michael Spring
Supervisors: Philippe Thévenaz, Michael Unser
SubjectDeconvolution with sparsity constraints
Zafer Dogan
Supervisors: Stamatis Lefkimmiatis, Michael Unser
SubjectEfficient algorithms for vector-field reconstruction
Emrah Bostan
Supervisors: Pouya Dehghani Tafti, Michael Unser
SubjectDisparity from multiscale monogenic phase
Christian Jaques
Supervisors: Kunal Chaudhury, Michael Unser
SubjectAnalyse du comportement de déversoirs dorage à laide dimagerie vidéo
Bergem Yannick
Supervisors: Daniel Sage, Michael Unser
SubjectImage denoising using dual formulations
Arnaud Le Carvennec
Supervisors: bourquard, Michael Unser
SubjectMorphological filtering via energy minimization
Emrah Bostan
Supervisors: bourquard, Michael Unser
SubjectDetermination of the Orientation of Tiles in Parallel-Scanning Microscopy
Marco Parisi
Supervisors: Philippe Thévenaz, Michael Unser, Bastien Rachet, bastien.rachet@epfl.ch, BM 4.118, Tel: 021 693 70 12
SubjectCell Tracking in Time-Lapse Microscopy
Mägli Raphaël
Supervisors: Ricard Delgado-Gonzalo, Michael Unser
SubjectCollagen filaments detection
François Curdy
Supervisors: Daniel Sage, Michael Unser, Alessandra Griffa, BIOP, EPFL
SubjectImage Denoising in Fluorescence Microscopy Using Several Acquisitions
Ulugbek Kamilov
Supervisors: Florian Luisier, Michael Unser, Daniel Sage
Subject3D deconvolution with non-conventional L1 regularization
Arnaud Le Carvennec
Supervisors: Raquel Terres Cristofani, Michael Unser, Aurélien Bourquard
Subject3D Nanoscale Structures in Living Cells
Youri Marko
Supervisors: Hagai Kirshner, Michael Unser
SubjectImplementation and comparison of keypoint detectors
Virginie Uhlmann
Supervisors: Daniel Sage, Michael Unser
SubjectConstrained reconstruction of fluorescent diffuse optical tomography (FDOT) data
Francis Géroudet, Master EPFL (MT)
Supervisors: Anonymous, Michael Unser, 1) Mathews Jacob, Universiy of Rochester, USA
SubjectRecalage de dendrites par plus proche voisin itéré
Eda Egüz
Supervisors: Jean-Charles Baritaux, Michael Unser
SubjectActive contours for segmentation of multilayered biological structures
Sambaturu Bhavani
Supervisors: Chandra Sekhar Seelamantula, Michael Unser
SubjectLinear estimation in Magnetic Resonance Imaging (MRI)
Laurent Lejeune
Supervisors: Guerquin-Kern Matthieu, Michael Unser
SubjectBilateral spline filters for image segmentation
Anil Yuce
Supervisors: Chandra Sekhar Seelamantula, Michael Unser, Daniel Sage
SubjectImage processing to facilitate Optical Character Recognition
Alexandre Tairum
Supervisors: Guerquin-Kern Matthieu, Michael Unser
SubjectDesign of a new heart phantom for cardiac MRI simulations
Isik Karahanoglu
Supervisors: Guerquin-Kern Matthieu, Michael Unser, Dimitri Van De Ville
SubjectHigh Dynamic Range Imaging
Nicolas Augier
Supervisors: Guerquin-Kern Matthieu, Michael Unser
SubjectiSkyline (Skyline Detection)
Silvan Widmer
Supervisors: Philippe Thévenaz, Michael Unser
SubjectEstimation of Local Aortic Elastic Properties with MRI
Mustapha Al Kharfane, SV
Supervisors: Ricard Delgado-Gonzalo, Michael Unser
SubjectFast space-variant Image Filtering - Applications to Fluorescence Microscopy Images
Zsuzsanna Püspöki
Supervisors: Daniel Sage, Michael Unser, Daniel Sage
SubjectCompensation of lipids signal in in-vivo MRSI using B-SLIM
María Navarro Leiva, Master Universidad de Málaga, Málaga
Supervisors: Dimitri Van De Ville, Michael Unser, Ildar Khalidov
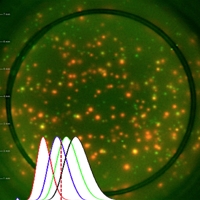
SubjectData Analysis for Photonic-Force Microscopy
Amardeep Singh, Master UniBwM, Munich
Supervisors: Philippe Thévenaz, Michael Unser
SubjectImage Processing Algorithms for Resolution Enhancement
Aurélien Bourquard, Master EPFL (MT)
Supervisors: Anonymous, Michael Unser
SubjectLego-ball polyharmonic B-splines, and the best wavelet pool ever !
Reza Shrivany, Master ENSEEIHT, Toulouse
Supervisors: Anonymous, Michael Unser
SubjectFast autocorrelation calculation methods for polyharmonic B-splines
Yann Barbotin
Supervisors: Dimitri Van De Ville, Michael Unser, Thierry Blu
SubjectDecision maps for tonotopic organization as revealed by fMRI
Yvette Bohraus
Supervisors: Dimitri Van De Ville, Michael Unser
SubjectEvolutionary snake algorithms for biological applications
Stefan Geissbuehler
Supervisors: Daniel Sage, Michael Unser, Chandra Sekhar Seelamantula
SubjectEstimation du déplacement des vagues par analyse d'images vidéos
Claire Verburgh
Supervisors: Daniel Sage, Michael Unser
SubjectSystème de visualisation pour la navigation à travers des très grandes images de microscopie
Francis Géroudet
Supervisors: Daniel Sage, Michael Unser
SubjectDigital quantitative phase recovery from focal series of brightfield microscopy images
Cecile Bucher
Supervisors: François Aguet, Michael Unser
SubjectDeconvolution in 3D: an ImageJ plugin
Guillaume Schmit, Master EPFL (MT)
Supervisors: Cédric Vonesch, Michael Unser
SubjectFitting of 3D-PSF models to fluorescent microbead stacks
Raphaël Frey, Master EPFL (MT)
Supervisors: Cédric Vonesch, Michael Unser
SubjectDenoising of MRS Signals Using Wavelet Methods
Nicole Brüschweiler, Master EPFL (MT)
Supervisors: Ildar Khalidov, Michael Unser
SubjectTime-course analysis of perfusion measurements in laser Doppler imaging
Alessandra Griffa, Master Politecnico di Torino, Turin
Supervisors: Dimitri Van De Ville, Michael Unser, Prof. Theo Lasser (LOB)
SubjectWavelet-based methods for the solution of inverse problems and de-noising
Matthieu Guerquin-Kern, ENS Cachan, Paris
Supervisors: Cédric Vonesch, Michael Unser
SubjectDemonstration applet for exponential B-splines
Patricia Signé (SSC)
Supervisors: Ildar Khalidov, Michael Unser
SubjectColor image Segmentation in Optical Microscopy
Joël Leuenberger
Supervisors: Daniel Sage, Michael Unser
SubjectQuantify vessels growing in the chloro-allantoic membrane by image processing techniques
Céline Di Venuto
Supervisors: Daniel Sage, Michael Unser
SubjectGranulométrie de vésicules lipidiques par snakuscules
Olivier Balagué
Supervisors: Philippe Thévenaz, Michael Unser
SubjectSupport vector machines for functional MRI
Daniel Boss
Supervisors: Dimitri Van De Ville, Michael Unser
SubjectSuppression de structures quasi-périodiques dans le domaine de Fourier
Jean-Paul Fuchs
Supervisors: Pouya Dehghani Tafti, Michael Unser
SubjectEtude de cellules adipeuses par analyse d'images en histologie
Sébastien Romain
Supervisors: Chandra Sekhar Seelamantula, Michael Unser
SubjectWavelet-based Denoising of 3D Microscopic Images
Saskia Delpretti
Supervisors: Florian Luisier, Michael Unser
SubjectAnalyse de traces de particules mobiles dans des images de biologie cellulaire
Xavier Winterhalter
Supervisors: Daniel Sage, Michael Unser
SubjectStructure des noyaux de neurones du cortex somato-sensoriel
Charlie Darricau
Supervisors: Philippe Thévenaz, Michael Unser
SubjectInterpolation avec compensation des non-idéalités d'échantillonnage
Aurélien Bourquard
Supervisors: Katarina Balać, Michael Unser, Philippe Thévenaz
SubjectFunctional connectivity analysis using wavelet-based statistical resampling
Robert Stachowiak
Supervisors: Dimitri Van De Ville, Michael Unser, Nouchine Hadjikhani
SubjectTracking cells with snake algorithms and Kalman filter
Jonathan Besuchet
Supervisors: Chandra Sekhar Seelamantula, Michael Unser
SubjectUn nuovo approccio di utilizzo della trasformata
Antonio Frutero, Master, Politecnico di Torino, Turin
Supervisors: Dimitri Van De Ville, Michael Unser
SubjectApplications des contours actifs à la trajectométrie d'un museau de souris
Laurent Gillet, Master EPFL (MT)
Supervisors: Philippe Thévenaz, Michael Unser
SubjectReconstruction 3D des réseaux vascualaires en imagerie médicale
Nicole Brueschweiler
Supervisors: Daniel Sage, Michael Unser
SubjectRéduction morphologique d'images
Nicolas Blanc
Supervisors: Philippe Thévenaz, Michael Unser
SubjectImageJ plug-in for fast denoising of noisy biological images
Ted Choueri
Supervisors: Sathish Ramani, Michael Unser
SubjectQuantitative measurement of chromatin condensation in 4D
Florent Cosandier
Supervisors: Daniel Sage, Michael Unser
SubjectValidation of 3D PSF models
Raphaël Frey
Supervisors: Cédric Vonesch, Michael Unser, Senior supervisor: Dimitri Van de Ville
SubjectAdaptive Wiener Filtering using Polyharmonic Wavelet Packets
Florian Vaussard
Supervisors: Dimitri Van De Ville, Michael Unser, Sathish Ramani
SubjectMulti-dimensional Non-Uniform Interpolation and Approximation for Robot Calibration
Olivier Blanc
Supervisors: Anonymous, Michael Unser, ildar.khalidov@epfl.ch, nuno.fazendacarrico@epfl.ch
SubjectDétourage de noyaux de cellule en imagerie par fluorescence
Lionel Flaction
Supervisors: François Aguet, Michael Unser
SubjectDémonstrateur Web pour la compréhension des images numériques
Thomas Lemmin
Supervisors: Daniel Sage, Michael Unser
SubjectFractal analysis of 3-D human skin data
Patrick Schoeneich
Supervisors: Dimitri Van De Ville, Michael Unser, Roland Michaely (LOB)
SubjectConstruction of a dendritic tree for neuroscience
Debasree Banerjee
Supervisors: Cédric Vonesch, Michael Unser
SubjectAnalysis of the myocardial wall thickness using snakes
Leos Urbanek
Supervisors: Philippe Thévenaz, Michael Unser, Michel Kocher
SubjectHigh-Resolution Techniques for Frequency Domain Optical Coherence Tomography
Himanshu Nazkani
Supervisors: Chandra Sekhar Seelamantula, Michael Unser, Prof. Rainer Leitgeb, Biomedical Optics Laboratory
SubjectThresholding strategies for image denoising with an application to fMRI statistical analysis
Florian Luisier, Master EPFL (MT)
Supervisors: Thierry Blu, Michael Unser
SubjectConnectivité corticale en imagerie de tenseurs de diffusion
David Lambiel, Master, Master EPFL (MT)
Supervisors: Philippe Thévenaz, Michael Unser
SubjectCalibration automatique pour caméra panoramique
Christophe Magnard, Master EPFL (MT)
Supervisors: Muthuvel Arigovindan, Anonymous
SubjectDéconvolution en microscopie dynamique
Pierre Besson, Master EPFL (MT)
Supervisors: Cédric Vonesch, Michael Unser, Francois Aguet
SubjectFast Non-Axisymmetric Drop Shape Analysis
Aurélien Stalder, Master EPFL (MT)
Supervisors: Daniel Sage, Michael Unser, Estelle Wagner, Gerit Kulik and Laura Barbieri (EPFL IOA)
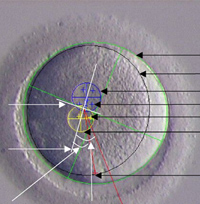
SubjectValidation de la méthode de scoring des zygotes par analyse d'images
Antoine Beuchat, Master EPFL (MT)
Supervisors: Muthuvel Arigovindan, Michael Unser
SubjectAnalysis of fMRI data using polyharmonic B-spline wavelets
Simplice Tchokouani, Master, MT, EPFL
Supervisors: Dimitri Van De Ville, Michael Unser
SubjectWavelet-based extended depth-of-field using hidden markov models
Alex Prudencio, Master, SSC, EPFL
Supervisors: Dimitri Van De Ville, Michael Unser, Cedric Vonesch
SubjectConception dondelettes à partir des B-splines polyharmoniques dans le cas non-séparable 2D
Matthieu Guerquin-Kern, ENS de Cachan, Paris
Supervisors: Dimitri Van De Ville, Michael Unser
SubjectTexture analysis for tumor histology images
Vincent Cattin
Supervisors: Anonymous, Anonymous
SubjectDétection de contour avec une précision sub-pixel
Nicolas Pavillon
Supervisors: Anonymous, Anonymous
SubjectReconstruction 3D des réseaux vascualaires en imagerie médicale
Jolyon Roth
Supervisors: Anonymous, Anonymous
SubjectApplet de démonstration pour le filtrage d'images chez Fourier
Joy Anushini Ariarajah
Supervisors: Ildar Khalidov, Anonymous
SubjectImageJ plug-in for noise reduction in functional imaging data
Alex Prudencio
Supervisors: Shai Tirosh, Anonymous, Dimitri Van De Ville
SubjectMesure de position en microscopie dynamique par fluorescence
Milan Stupar
Supervisors: François Aguet, Anonymous
SubjectSuivi de vibrisses de souris pour l'étude du comportement sensoriel chez l'animal
Loic Segapelli
Supervisors: Daniel Sage, Michael Unser
SubjectCalibrage cinématique dun robot à 6 degrés de liberté par des B-splines cubiques
Niklaus Hugi
Supervisors: Ildar Khalidov, Michael Unser, Nuno Fazenda ME B3 484, Tel: 33824
SubjectAnalyse structurale 3D de roches fracturées : application géologique de la XRCT
Jean Keomany
Supervisors: François Aguet, Michael Unser
SubjectNeuron tracing in 3D
Joël Arnold
Supervisors: Cédric Vonesch, Michael Unser
SubjectIdentification de glomérules par analyse d'image du système olfactif
Anna Larsson
Supervisors: Daniel Sage, Michael Unser
SubjectAutostéréogrammes par B-splines
Basile Graf
Supervisors: Philippe Thévenaz, Michael Unser
SubjectRetouche d'images: suppression des lignes électriques dans les photos
Julien Reuse
Supervisors: Sathish Ramani, Michael Unser
SubjectPolyharmonic wavelets for a dyadic subsampling scheme
Azzabi Zouraq Salim
Supervisors: Dimitri Van De Ville, Michael Unser
SubjectTrajectométrie de souris pour des études de comportement en neuroscience
Sadasing Kowlessur
Supervisors: Daniel Sage, Michael Unser
SubjectImageJ plug-in for polyharmonic wavelet transform
Cristina Manfredotti, Master, Università di Milano, Milan
Supervisors: Dimitri Van De Ville, Michael Unser
SubjectCorrection les effets de la PSF en imagerie spectroscopique
Mathieu Vonlanthen, Master, MT, EPFL
Supervisors: Dimitri Van De Ville, Michael Unser
SubjectGeneralized Daubechies wavelets
Cédric Vonesch, Master, SSC, EPFL
Supervisors: Thierry Blu, Michael Unser
SubjectNouvelle génération d'ondelettes orientables - Application à la réduction de bruit en IRM fonctionnelle
Jesse Berent, Master, MT, EPFL
Supervisors: Brigitte Forster, Michael Unser, Thierry Blu, BM 4.134, Tel: 35172
SubjectAnalyse d'image pour l'étude de la dynamique de cellules souches
Fabien Saint-Roch, Master, IN, EPFL
Supervisors: Daniel Sage, Michael Unser
SubjectA versatile tool for 3D wavelet processing
Avo Rasolondraibe, Master, IN, EPFL
Supervisors: Dimitri Van De Ville, Michael Unser
SubjectRedundant wavelet processing of fMRI data
Jean-Marc Luneau, Master, Université de Nice, Nice
Supervisors: Dimitri Van De Ville, Michael Unser
SubjectThree-dimensional surface recovery from microscopy images using object model-based deconvolution
Francois Aguet, Master, IN, EPFL
Supervisors: Dimitri Van De Ville, Michael Unser
SubjectMicroscope virtuel à but didactique pour Internet
Chistophe Magnard
Supervisors: Rajesh Langoju, Michael Unser
SubjectTraitement d'images en microscopie électronique pour la nano-fabrication
Christian Ban
Supervisors: Shai Tirosh, Michael Unser, Tristan Bret, APL, EPFL, BM 4.108, Tel 35716
SubjectAnalyse d'une séquence d'images pour la caractérisation de traitement de surface
Aurélien Stalder
Supervisors: Daniel Sage, Michael Unser, Laura Barbieri
SubjectAssemblage et homogénéisation d'images pour les neurosciences
Raphaël Tornay
Supervisors: Daniel Sage, Michael Unser
SubjectAnalyse de texture basée sur de filtres orientables
Pierre Besson
Supervisors: Philippe Thévenaz, Michael Unser
SubjectConstruction of topological maps from a series of multi-focal images
Niels Quack
Supervisors: Brigitte Forster, Michael Unser
SubjectLocalisation de chromosomes à travers une série d'images de microscopie en fluorescence
Annick Marin
Supervisors: Daniel Sage, Michael Unser
SubjectImagerie 3D par transformée en ondelettes continue
Thierry Bernhard
Supervisors: Michael Liebling, Michael Unser, Luc Froehly, LOB, EPFL, BM 5.140, Tel: 37773
SubjectCréation de mosaïque d'images en imagerie biomédicale
David Lambiel
Supervisors: Philippe Thévenaz, Michael Unser
SubjectInterpolation d'images haute qualité basée sur des splines explonentielles
Pierre-Yves Schuetz
Supervisors: Ildar Khalidov, Daniel Sage
SubjectAnalyse de texture basée sur ondelettes
Mathieu Vonlanthen
Supervisors: Dimitri Van De Ville, Michael Unser
SubjectTraitement d'images pour la caractérisation d'ovocytes
Antoine Beuchat
Supervisors: Carlos Óscar Sánchez Sorzano, Michael Unser
SubjectRelevé de l'arbre dendritique dans des images confocales 3D
Florian Marty
Supervisors: Michael Sühling, Daniel Sage
SubjectComplex splines and wavelets
Florian Luisier
Supervisors: Thierry Blu, Michael Unser, Thierry Blu
SubjectModélisation des taches d'un gel électrophorétique par mixture et/ou par dictionnaire de fonctions de base
Christophe Gusthiot
Supervisors: Philippe Thévenaz, Michael Unser
SubjectDétection de molécules d'ADN avec des filtres orientables
Alwyn Fernandes
Supervisors: Mathews Jacob, Michael Unser
SubjectDétection de lésions hépatiques
Reza Etemad-Sajadi
Supervisors: Nadia Subotić, Michael Unser
SubjectDétection d'objets dans des images par une procédure d'optimisation Application en biologie moléculaire
Dave Bergomi
Supervisors: Slavica Jonić, Michael Unser
SubjectReconnaissance automatique de la texture pulmonaire
Vahid Fahfouri
Supervisors: Daniel Sage, Michael Unser
SubjectSynthèse d'images et détermination de la topologie par fusion de série focale
Jesse Berent
Supervisors: Brigitte Forster, Michael Unser, Daniel Sage
SubjectLissage directionnel rapide pour le traitement d'images biologiques
Philippe Portmann
Supervisors: Philippe Thévenaz, Anonymous
SubjectCorrection des déformations optiques pour une caméra panoramique
Beda Steinacher
Supervisors: Muthuvel Arigovindan, Michael Unser
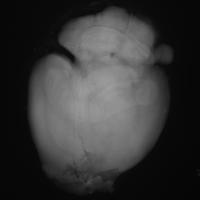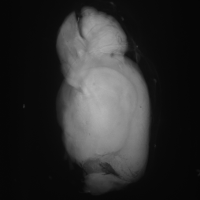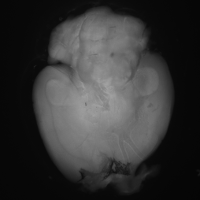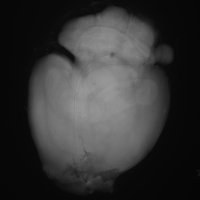
SubjectChamp de déformation d'un coeur qui bat
Wolf Blecher
Supervisors: Philippe Thévenaz, Michael Unser
SubjectPoursuite de neurones dans une séquence d'images
Vincent Ducry
Supervisors: Daniel Sage, Michael Unser
SubjectDétecteur de structure orientable et paramétrisable: application à l'analyse d'images biomédicales
François Aguet
Supervisors: Mathews Jacob, Anonymous
SubjectGeodesic Active Contours and Splines
Shai Tirosh, Doctorate school, SSC, EPFL
Supervisors: Mathews Jacob, Michael Unser
SubjectTracking fluorescence within cells
Nadja Subotic, Doctoral school, SSC, EPFL
Supervisors: Dimitri Van De Ville, Michael Unser
SubjectOptical Coherence Tomography (OCT): A superresolution method
Herbert Bay, Master, MT, EPFL
Supervisors: Thierry Blu, Michael Unser
SubjectNavigation system for Abdominal Aortic Aneurysm
Michaël Rochat, Master, MT, EPFL
Supervisors: Anonymous, Michael Unser
SubjectNumerical Reconstruction of semi-transparent objects in Optical Diffraction Tomography
Asma Jebali, Master, MT, EPFL
Supervisors: Michael Liebling, Michael Unser
SubjectImage matching in Java
Fabien Julliard, Master, MT, EPFL
Supervisors: Philippe Thévenaz, Michael Unser
SubjectTracé d'arbre dendritique
Sylvain Anderegg
Supervisors: Erik Meijering, Michael Unser
SubjectAnalyse en composantes principales : application à la caractérisation dovocyte pour la fécondation in-vitro
Antoine Beyeler
Supervisors: Muthuvel Arigovindan, Michael Unser
SubjectCorrection des images et réduction du bruit dautofluorescence en microscopie par fluorescence
Pascal Geiser
Supervisors: Mathews Jacob, Michael Unser
SubjectDéballage de phase pour la reconstruction des hologrammes digitaux
Pande Mitrev
Supervisors: Michael Liebling, Michael Unser
SubjectDétection de molécules dADN dans des images de cryo-microscopie électronique
Jacques Neuenschwander
Supervisors: Michael Sühling, Michael Unser
SubjectAnalyse dimage pour la détection de syncytia en thérapie anti-VIH
Ambroise Krebs
Supervisors: Daniel Sage, Michael Unser
SubjectDétection de chocolats par Watershed
Daniel Stadelmann
Supervisors: Daniel Sage, Michael Unser
SubjectCaractérisation de microstructures osseuses par analyse dimages
Pierre Roduit
Supervisors: Slavica Jonić, Michael Unser
SubjectImagerie paramétrique du cur
Rui Protasio
Supervisors: Philippe Thévenaz, Michael Unser
SubjectDétection de microcalcifications en mammographie
Céline Costamagna
Supervisors: Manuela Feilner, Michael Unser
Subject3D reconsruction from multiple views
Alexandre Goy
Supervisors: Thierry Blu, Michael Unser
SubjectDetection of vascular diameters by ultrasonic imaging
Roland Michaely
Supervisors: Daniel Sage, Michael Unser
SubjectSegmentation and visualization of blood vessels obtained by 3D rotational angiograph
Laurent Vieira de Mello
Supervisors: Erik Meijering, Michael Unser
SubjectNew algorithm of wavelet transform
Gil Gaillard, Master, MT, EPFL
Supervisors: Manuela Feilner, Michael Unser
SubjectMosaicing en microscopie optique
Olivier Balsiger
Supervisors: Thierry Blu, Michael Unser
SubjectTransformées d'images en Java sur le web
Louis-Séverin Bieri
Supervisors: Slavica Jonić, Michael Unser
SubjectMovie creation from a mosaic of images
Emilio Casanova
Supervisors: Thierry Blu, Michael Unser
SubjectImage Processing applied on micro-arrays for molecular biology
Sacha Haymoz
Supervisors: Daniel Sage, Michael Unser
SubjectQuincunx Wavelet Transform with Fractional Filters
Asma Jebali
Supervisors: Manuela Feilner, Michael Unser
SubjectZoom in Java
David Leroux
Supervisors: Arrate Muñoz Barrutia, Michael Unser
SubjectMesure de similitude: Implémentation à l'aide d'invariants
Antoine Luisier
Supervisors: Thierry Blu, Michael Unser, Antoine Luisier
SubjectCorrection des distorsions géométriques d'une WebCam
Philippe Margairaz
Supervisors: kybic, Michael Unser
SubjectComparaison de méthodes d'interpolation - Applet de démonstration en Java
Raphaël Marthe
Supervisors: Slavica Jonić, Michael Unser
SubjectImage Processing on Microarrays
Delphine Perrottet
Supervisors: Daniel Sage, Michael Unser
SubjectAdaptative Spline Smoothing
Thomas Peter
Supervisors: Arrate Muñoz Barrutia, Michael Unser
SubjectNoise Reduction in Holographic Microscopy Images
Micael Rochat
Supervisors: Michael Liebling, Michael Unser
SubjectRotation chez Fourier
Patrick Servet
Supervisors: Philippe Thévenaz, Michael Unser
SubjectFunctional morphological evolution of neurones in culture
Anil Swaroop
Supervisors: Mathews Jacob, Michael Unser
SubjectTransformées en ondelettes par décomposition en B-splines
Raphaël Ertle, Doctorate school, SSC, EPFL
Supervisors: Arrate Muñoz Barrutia, Michael Unser
SubjectComputerized tomography
Michael Liebling, Master, PHY, EPFL
Supervisors: horbelt, Michael Unser
SubjectProbability density estimation using spline
Tatsuhei Iwasaki, École Polytechnique, Paris
Supervisors: Thierry Blu, Michael Unser
SubjectSegmentation of biomedical images and volumes
Gil Gaillard
Supervisors: kybic, Michael Unser
SubjectAnalyse et synthèse de texture
Svend Hoyer
Supervisors: Manuela Feilner, Michael Unser
SubjectEtude du langage par IRMF
Jean-Michel Pignat
Supervisors: Manuela Feilner, Michael Unser
SubjectJava-bases computer tomography reconstruction by filtered backprojection using B-Spline
Martin Demierre
Supervisors: horbelt, Michael Unser
SubjectConception d'un snake en utilisant une connaissance a priori
Issam El Bakkouri, École Polytechnique, Paris, France
Supervisors: Thierry Blu, Michael Unser
SubjectCharacterisation of approximation properties of finite elements
Sylvia Garcia
Supervisors: Thierry Blu, Michael Unser
SubjectRéduction de bruit dans des images biomédicales par des algorithmes pyramidaux et par des ondelettes
Cédric Glauser
Supervisors: Manuela Feilner, Michael Unser
SubjectCompensation of the retina motion
Mourad Kharouf
Supervisors: Philippe Thévenaz, Anonymous
SubjectDetection of contours in biomedical images using
Bernhard Petersch
Supervisors: Daniel Sage, Michael Unser
SubjectDetection of contours in biomedical images using dynamic programming
Bernhard Petersch
Supervisors: Daniel Sage, Michael Unser
SubjectCharacterisation of motion in a sequence of echocardiographic images
Yves Ramseier
Supervisors: kybic, Michael Unser
SubjectImplementation of fractional splines filters for wavelet transforms
Olivier Saudan
Supervisors: Thierry Blu, Michael Unser
SubjectChangement d'échelle fractionnaire
Mohamed Ali Mechhidan, École Polytechnique, Paris
Supervisors: Thierry Blu, Michael Unser
Subject